こんにちは、シュントです。
前回に引き続き、例題を使って、三角比の$\tan\theta$についてやっていきます。もし、$\sin\theta$や$\cos\theta$がわからない人がいれば、先に『数学Ⅰ 三角比1』をご覧になられることをおすすめします。
それではやっていきましょう!
今回も同様、最初は解けないはずなので、解答をみて、そこから見えてくる特徴をどんなことでもいいので、書き出してみるといいですよ!
例題と解答

例題と解答を照らし合わせてみるとどうですか?
まず、前回から、本当に有名角しか出てないことにお気付きでしょうか。
三角比では有名角がほとんどです。なので、三角比の本質さえつかめばとても簡単だということです!
今回は例題が少なめですので、法則性を見つけることが難しいかもしれませんが、前回の例題と解答も含めて考えると、やはり、$0$、$1$、$\sqrt{3}$というような数が出てきていますね。
「定義なしってどういうこと?」って思われたかたもいるかもしれませんが、これは後ほど説明しますね。とりあえず答えはないと思っておいてください。
では、気付くポイントの例として、以下にまとめておきました。(今回はあまりなかったかもしれません。)
・$0$、$1$、$\sqrt{3}$という数がよく出る。
・有名角しかない。
など
今回の例題も、たったこれだけで終わりです!
三角比の説明($\tan\theta$)
まず、$\tan\theta$をひとことでいうと、
傾き です!
どこの傾きかというと、下の図の三角形の斜辺(青線部)の傾きのことを$\tan\theta$といいます。
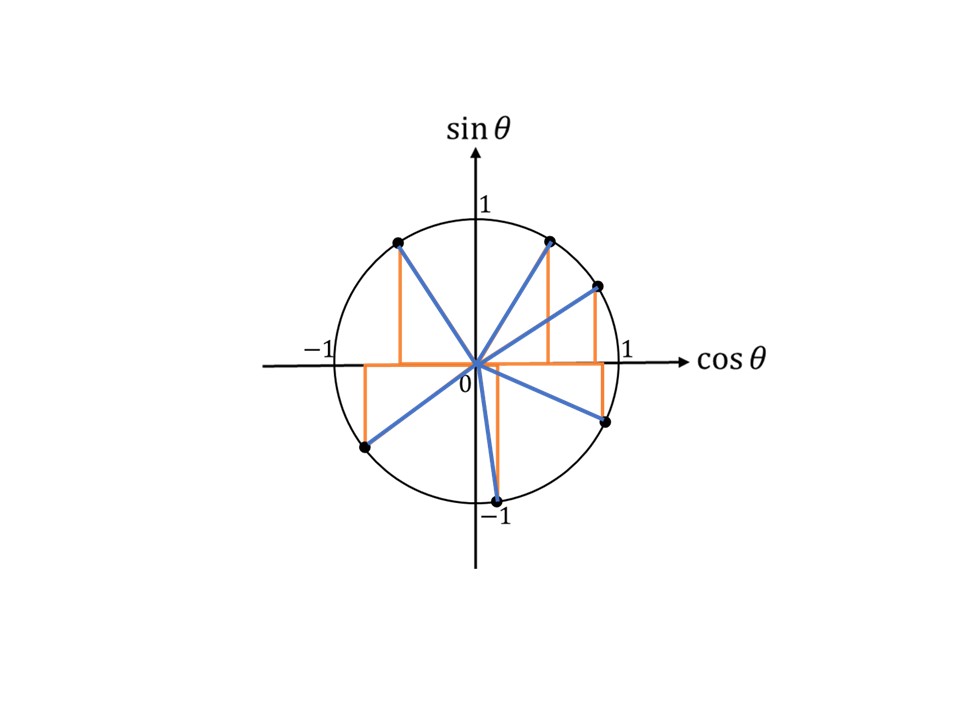
傾きと聞くとみなさんは何を思い浮かべますか。
そうですよね。
$傾き=\frac{yの変化量}{xの変化量}$
です!
2次関数などでおなじみの傾きです。
そして、前回にも言いましたが、$x$と$y$はいわゆる$\cos\theta$と$\sin\theta$のことでした。
ということは、次のように書き換えられます。
$\tan\theta=\frac{\sin\thetaの変化量}{\cos\thetaの変化量}$
ここで、変化量とは下の図のように、ある2点を取ってくることで求めることができます。
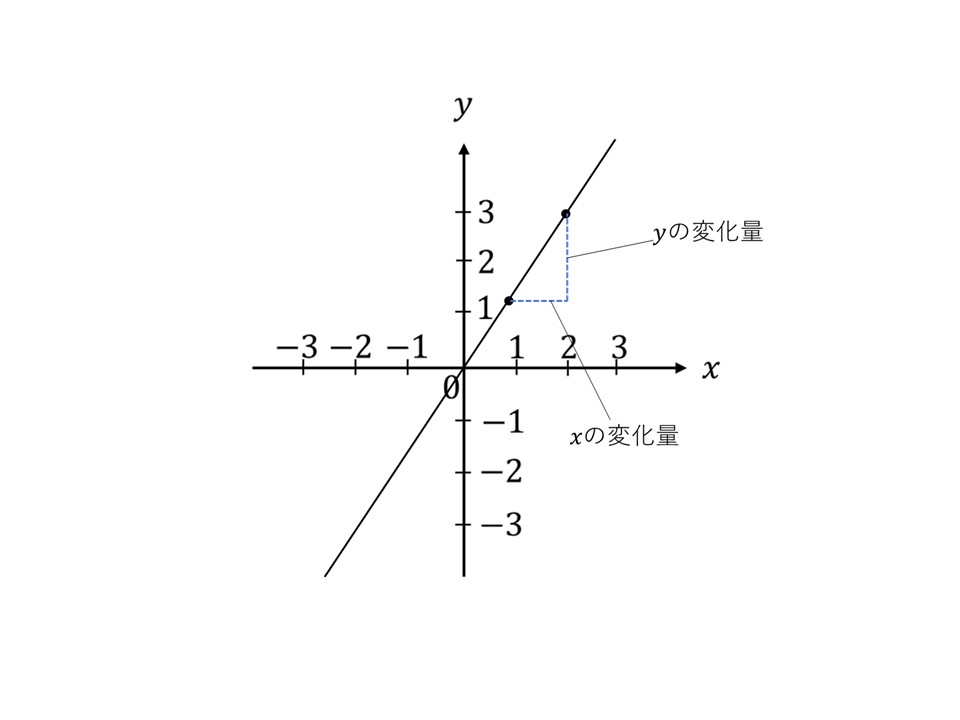
ですが、下の図のように、$\sin\theta$も$\cos\theta$も座標の$0$からの値でしたよね。
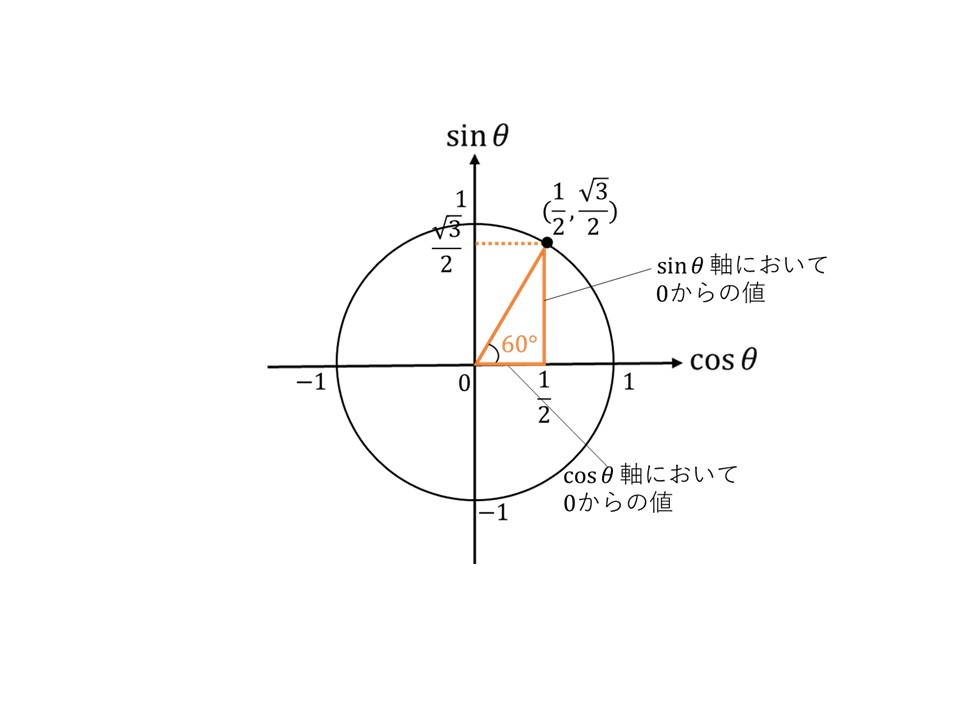
なので、$\sin\theta$と$\cos\theta$の値は常に、ある2点そのものを表しています。式では次のように書くことができます。
$\tan\theta=\frac{\sin\theta-0}{\cos\theta-0}$
$0$を省略すると、
$\tan\theta=\frac{\sin\theta}{\cos\theta}$
これは、よく使う三角比の公式です。教科書では三角比の相互関係の公式のひとつとして載せられていますね。
そして、$\tan\theta$が何を表しているのかもわかりましたね。
例題(1)では$\cos0°=1$、$\sin0°=0$より
$\tan0°=\frac{\sin0°}{\cos0°}=\frac{0}{1}=0$
です。
例題(2)では$\cos30°=\frac{\sqrt{3}}{2}$、$\sin30°=\frac{1}{2}$より
$\tan30°=\frac{\sin30°}{\cos30°}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$
です。
といった感じで$\tan\theta$も$\sin\theta$や$\cos\theta$と同様に求めることができるようになりました。
ちなみにですが、$\tan90°=∞$となっていますよね。これは傾きが、とーっても大きいという意味なんです。傾きのある坂を想像してみてください。傾き$5°$、$30°$、$45°$、$60°$の坂があったとします。もちろん、数学では$\tan\theta$の値は角度が大きくなるにつれて大きくなっていきます($0°\leq\theta\leq90°$のとき)。ということは、傾きが$90°$あたりで、傾きは最大値を取りそうですよね。ですが、どんどん大きくなる値に限度を設けることができません。数値では表現できませんが、ただわかっていることは限りなく大きくなるということです。よって、無限大と表現したり定義なしと表現します。
それともうひとつ!
教科書では、よく$\tan\theta$をグラフから求めるときに、下の図のように、$\sin\theta$軸に平行な線分を$\cos\theta=1$のところに引いて、さらに三角形の斜辺を延長し、さっき引いた線分と交わる点の$\sin\theta$の値が$\tan\theta$と表現していることが多いです。
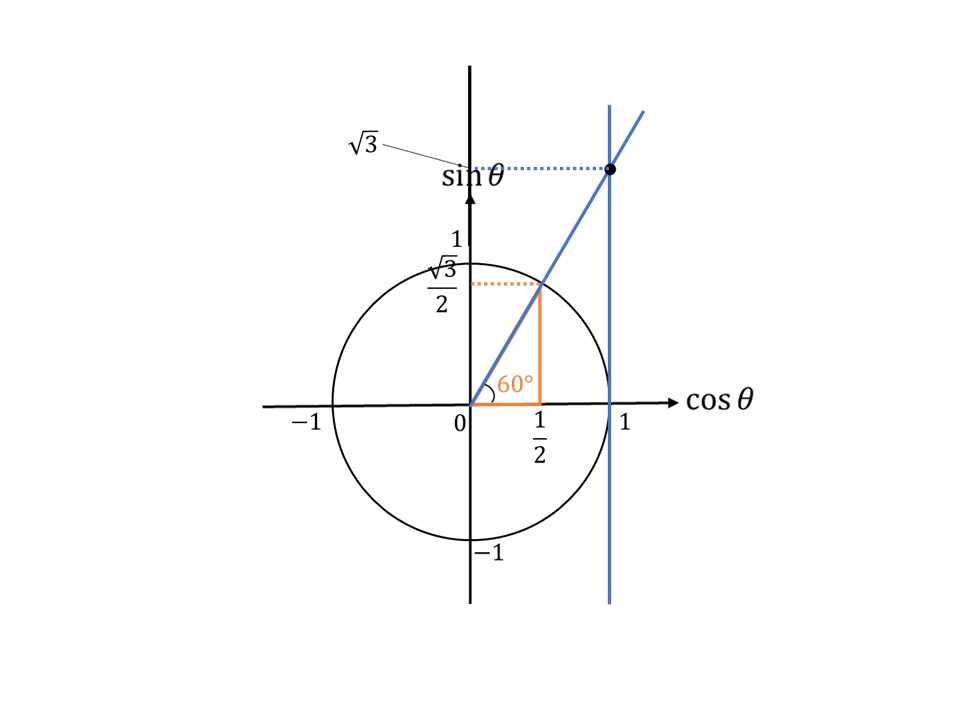
これがどういうことかというと、$\tan\theta=\frac{\sin\theta}{\cos\theta}$の式の$\cos\theta$の値を$1$にすることで、次のような式が成り立つのです。
$\tan\theta=\frac{\sin\theta}{1}=\sin\theta$
この考え方は、全く数学的ではありません。なぜなら、あたかも常に$\tan\theta=\sin\theta$が成り立つかのように誤解させ、さらに、せっかく三角比という斜辺の大きさを$1$にして、全員が同じ三角形を想像できるように、定義し便利にしたのに、それを無視しています。こういった考え方は本質を知った上で、理解することは良いですが、はじめて三角比を学ぶ者にとっては不適切だと考えます。
なので、みなさんはとにかく、$\tan\theta$は傾きであり、$\sin\theta$の変化量と$\cos\theta$の変化量から求めることができるということだけ知っておいてください。
三角比の相互関係
ここからは、よく教科書でもみる三角比においての公式です。
公式と聞くと覚えるのが大変と思うかもしれませんが、
大丈夫です!めっちゃ簡単なので!
三角比の相互関係は主に二つあります。そのうちひとつの式を変形して、三つの公式として紹介されることが多いです。
そして、ひとつは先ほど言ったように、すでに出てきています。
$\tan\theta=\frac{\sin\theta}{\cos\theta}$
これですね。
もう一つは、三平方の定理を使ったものです。今まで三角比では、下の図のように直角三角形を用いて考えていました。
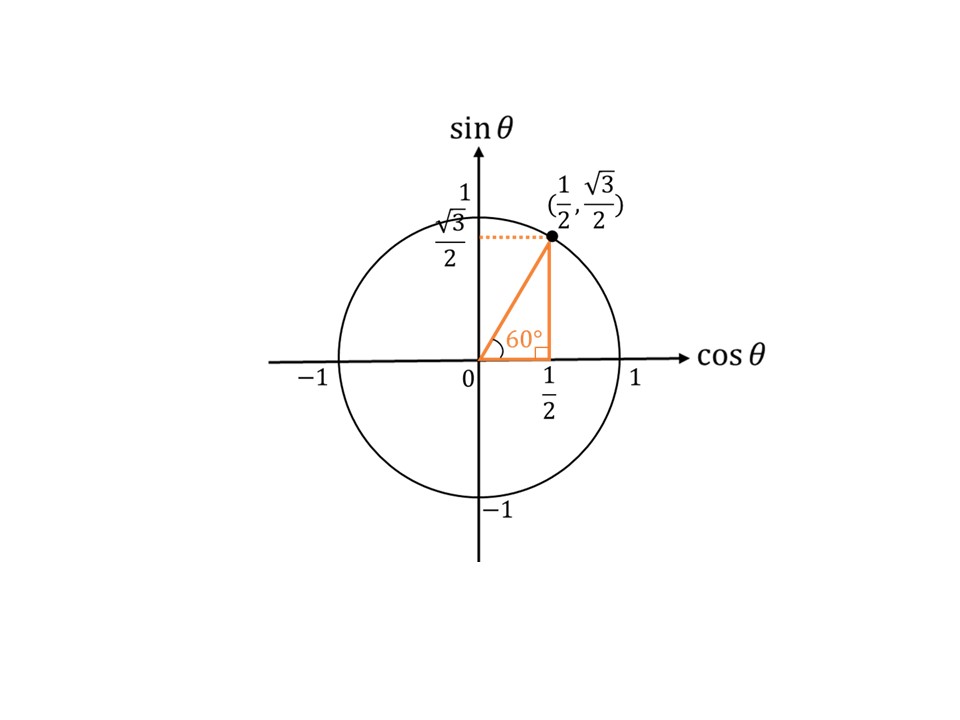
お気付きだと思いますが、直角三角形ですよ!もちろん三平方の定理を適用することができます。
三平方の定理はこんなんでしたね!
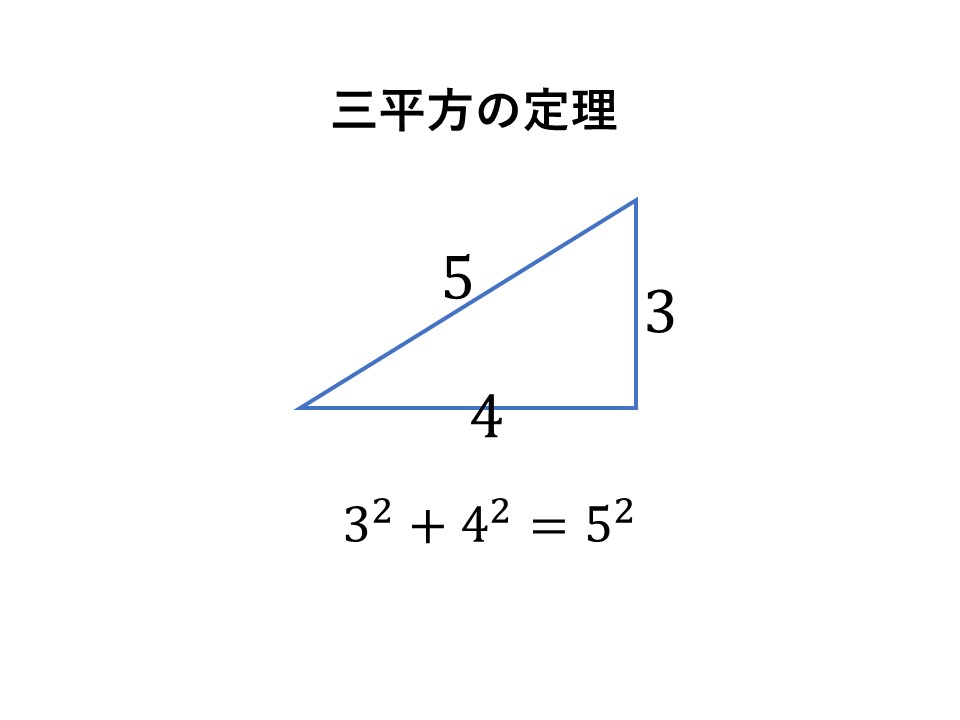
それと同じ考えをすると、三角比ではこんな感じに表せます。
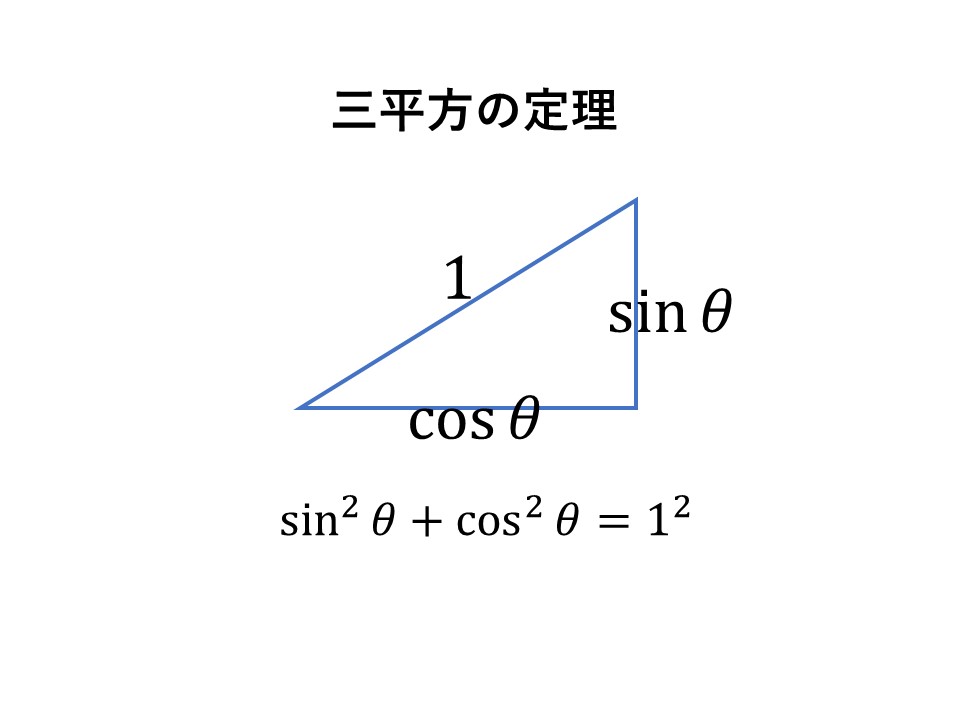
上の図にも書いていますが、ここで三平方の定理を適用すると、次のようになります。
$\sin^2\theta+\cos^2\theta=1$
これが三角比の相互関係の二つ目です。簡単でしたよね。
もう一つは何かというと、この二つ目の三角比の相互関係の式を変形しただけです。どんな変形かというと、式の両辺に$\frac{1}{\cos^2\theta}$を掛けるんです!
すると次のようになります。
$1+\tan^2\theta=\frac{1}{\cos^2\theta}$
本当に変形しただけでしたでしょ?(笑)。でもこれが三つ目の三角比の相互関係です。
下にまとめました!
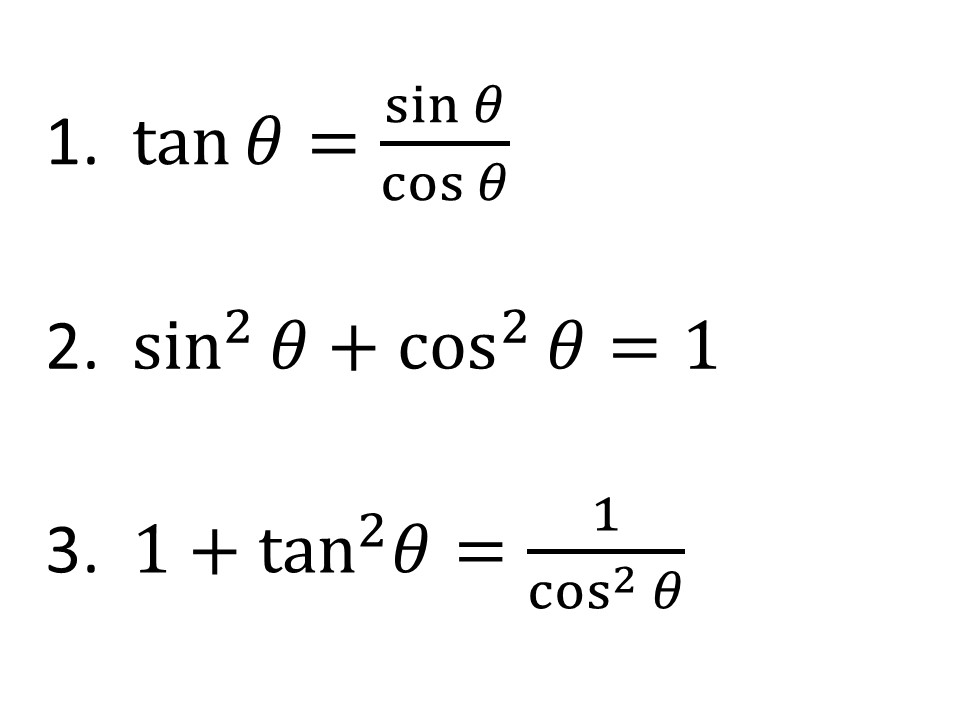
よって、覚えるのは二つ目までで十分です。式3は式2を変形すれば求められる、ということだけ覚えておきましょう。
最後に
これで、三角比の$\sin\theta$、$\cos\theta$、$\tan\theta$のすべてについて説明をしました。ですが、三角比で学ぶことはまだまだたくさんあります。これらの知識を使ってこれからいろんな例題を解いていきましょう!
次回は$0°\leq\theta\leq180°$に拡張したときについて話していこうと思います!


コメント