こんにちは、シュントです。
ここでは、例題をたくさん解いていくことで、三角比を理解できるようにします。
三角比の単元において、苦手意識を持つのは$\sin\theta$や$\cos\theta$や$\tan\theta$の記号が出てくるからではないでしょうか。ですが、これらの記号の詳しい説明、性質や定理は後にして、最初に最低限のことだけを教えるので、それだけで例題に取り組んでみましょう。
きっと解けないはずなので、解答をみて、そこから見えてくる特徴をどんなことでもいいので、書き出してみましょう。
三角比の定義
ここで、先ほど言った最低限のことについて話します。まず、$\sin\theta$や$\cos\theta$の$\theta$には分度器などでおなじみの角度が入ります!
そして、三角比の定義を以下に示します。この定義は覚えましょう。
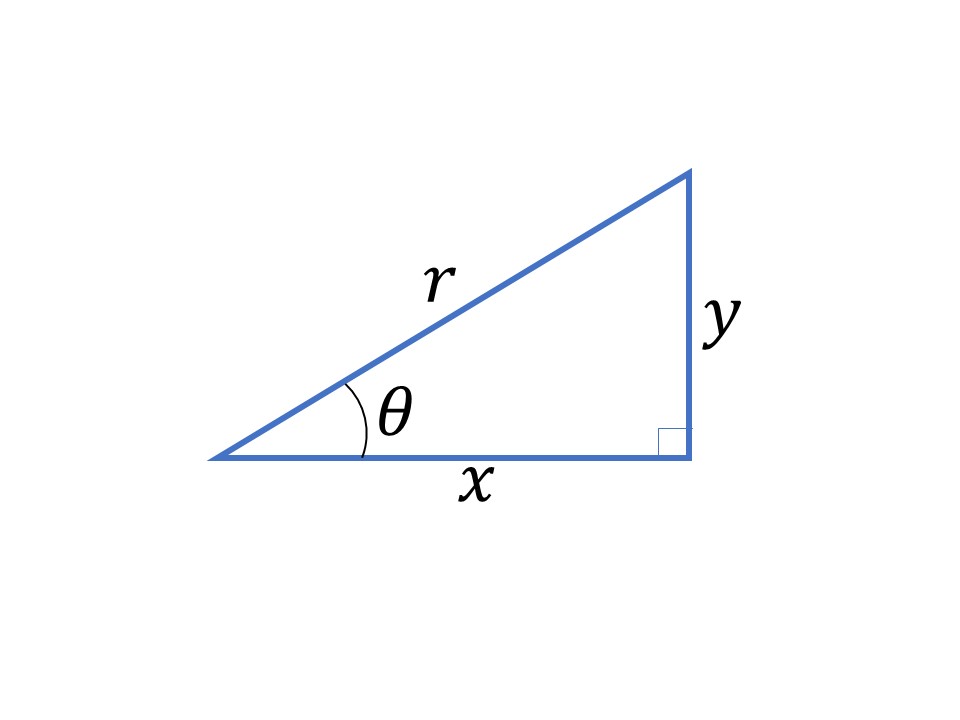
上の図のような、ある直角三角形があるとき、
$\sin\theta=\frac{y}{r}$
$\cos\theta=\frac{x}{r}$
$\tan\theta=\frac{y}{x}$
と定義します。
そして、これらそれぞれを$\theta$の
正弦(sine)
余弦(cosine)
正接(tangent)
とよびます。
三角比や三角関数を解いていくうちにだんだんこの定義にした理由が感覚的に身につくので、一旦覚えましょう。
例題と解答
それでは三角比の例題を解いてみましょう!
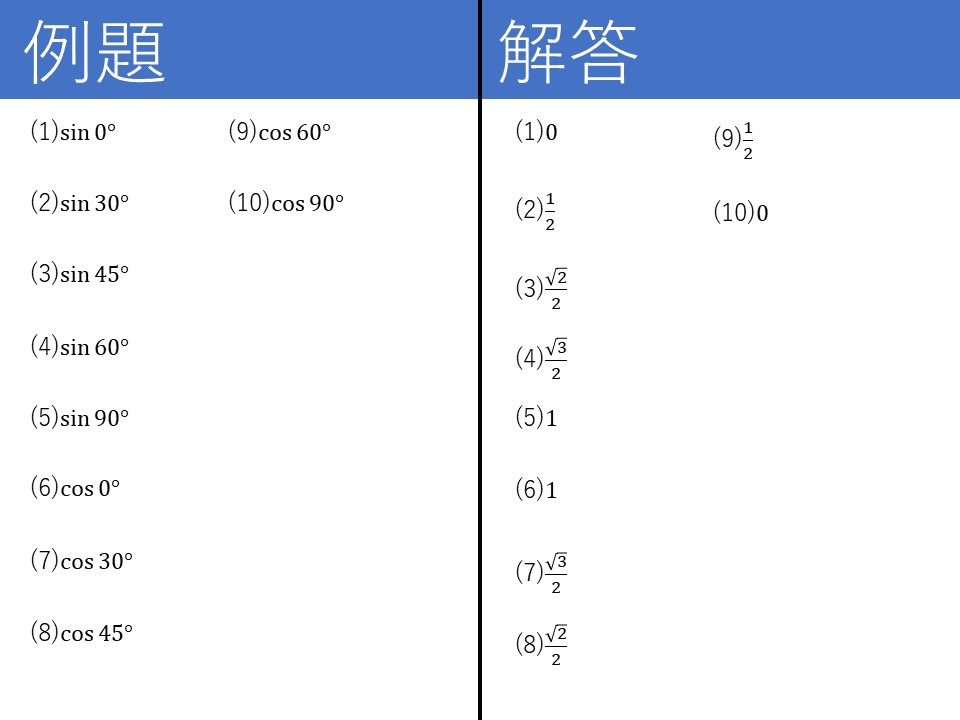
例題の解答と照らし合わせてみると、$0$、$1$、$\frac{\sqrt{2}}{2}$、$\frac{\sqrt{3}}{2}$という数が頻出ということに気が付きませんか。
そうなんです。三角比という単元においてこれらの数はとても大切なのです。なぜ、これらの数が大切なのかということを説明する前に$\frac{1}{2}$、$\sqrt{2}$、$\sqrt{3}$がどのくらいの大きさなのか少数で表現してみると、それぞれ$0.5$、$1.41421\cdots$、$1.73205\cdots$です。よって、$\frac{\sqrt{2}}{2}=0.70710$、$\frac{\sqrt{3}}{2}=0.86602$となります。これらの数字の大体の大小は覚えておきましょう。
すると、もう一つ気が付くことがあると思います。それは、この例題のすべての解答が$0$以上$1$以下になっているということです。
気付くポイントの例として、以下にまとめておきました。
・$0$、$1$、$\frac{1}{2}$、$\sqrt{2}$、$\sqrt{3}$という数がよくでる。
・すべての解答が$0$以上$1$以下になっている。
・$\sin\theta$と$\cos\theta$の解答がなんとなく対象になっている。(例$\sin30°$と$\cos60°$が同じ値で$\sin60°$と$\cos30°$が同じ値)
など
今回の例題は、たったこれだけで終わりです!この例題からどんどん掘り下げていきますよ~
三角比の説明($\sin\thetaと\cos\theta$)
まず、$\sin\theta$と$\cos\theta$は後にわかりますが、よく
$\sin\theta$は座標の大きさが1までの$y$軸
$\cos\theta$は座標の大きさが1までの$x$軸
として扱うことが多いです。もちろんこれには訳があります。(後で説明しますね。)
まずは図でみるとはやいでしょう!
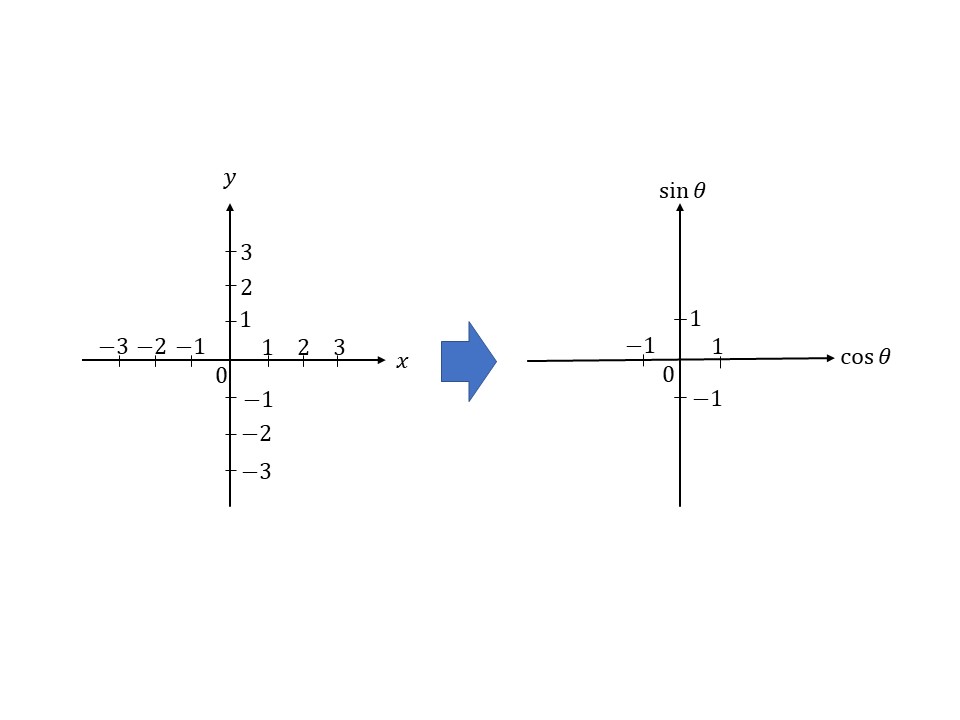
とても簡単でしょう?
一般的な$xy$グラフでは座標の点を表すときに、$(x,y)$と表しますよね?それは、次の図のように、点$(3,2)$であれば、$x$軸と$y$軸に対して、それぞれ垂線を引き、交わったところの数のことを表していました。
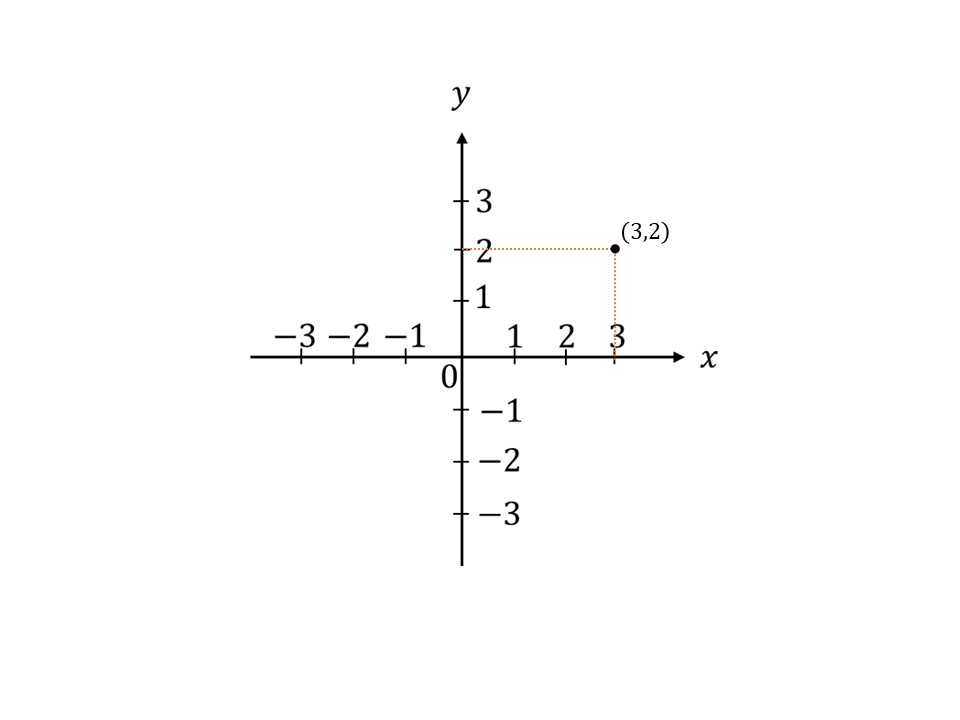
もちろん、このことは$\sin\theta$軸と$\cos\theta$軸のときにも同じことがいえます。ですが、座標の大きさがどちらの軸も$1$なので、グラフのとる値というのは、
$-1\leq\sin\theta\leq1$
$-1\leq\cos\theta\leq1$
という範囲の制限がありますが、考え方は同じです。
では、例題の(2)の$\sin30°=\frac{1}{2}$はどういう意味でしょうか。もうわかりましたよね?
$\theta$には度が入るので、$\sin30°=\frac{1}{2}$は$\theta$が$30°$のときの$y$軸の値は$\frac{1}{2}$と読み替えればいいのです。
ここで、つっこみたくなりますよね。
「$\theta$ってどこの角度やねん!」って
$\theta$は次の図に示したところなんです!
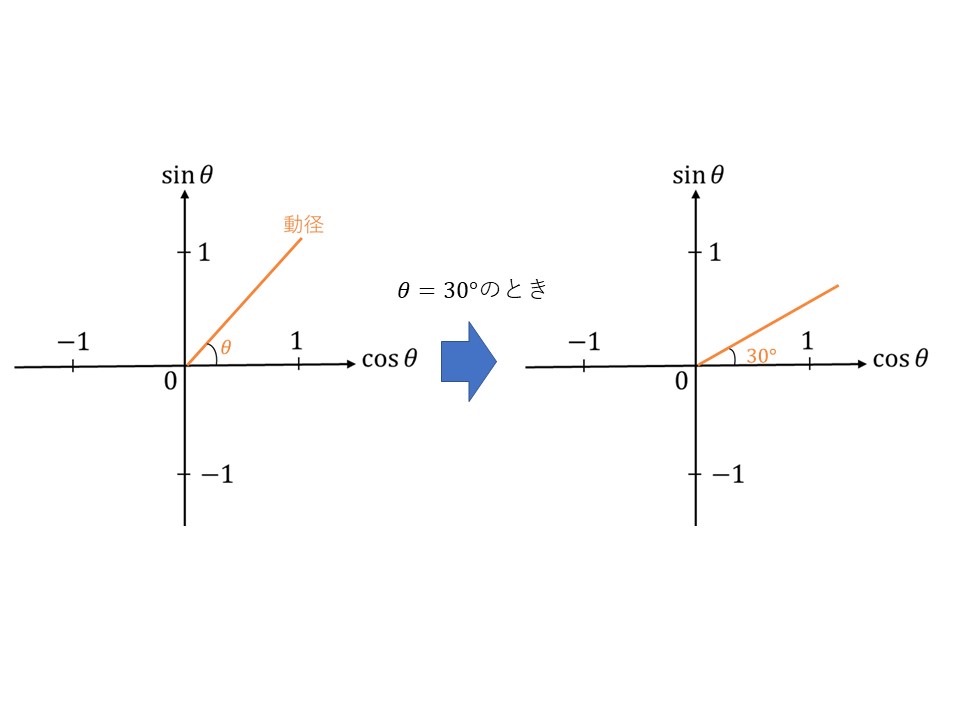
ですが、これだけでは$xy$座標のときのように点は定まっていません。そこで次の図のオレンジ色の枠で囲った、動径とそこから$\cos\theta$軸に対して下した垂線との三角形を考えるのです!
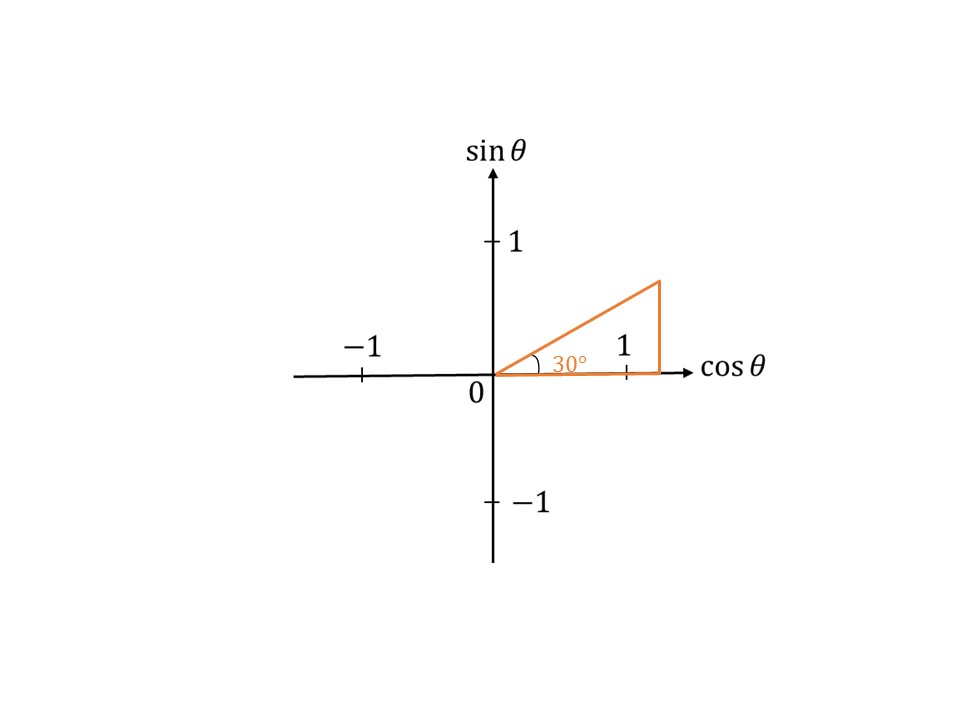
ここで思い出してください。$\sin\theta$も$\cos\theta$も範囲があって、それぞれ$-1\leq\sin\theta\leq1$、$-1\leq\cos\theta\leq1$でした。ということはこの範囲を超えないためには三角形の最大の辺が$-1$以上$1$以下であればいいのです。もっといえば、動径は$0$からなので、三角形の最大の辺の長さが$1$であればいいのです。
では、三角形の最大の辺とは何でしょう。それは、この作り方の三角形であれば必ず直角三角形になるので、斜辺が最大の辺になります。つまり、動径の大きさが$0$以上$1$以下であればいいということです。ですが、三角比や三角関数では動径の大きさを$1$として考えます。動径の大きさを$1$にしたときの三角形の図がこちらです。
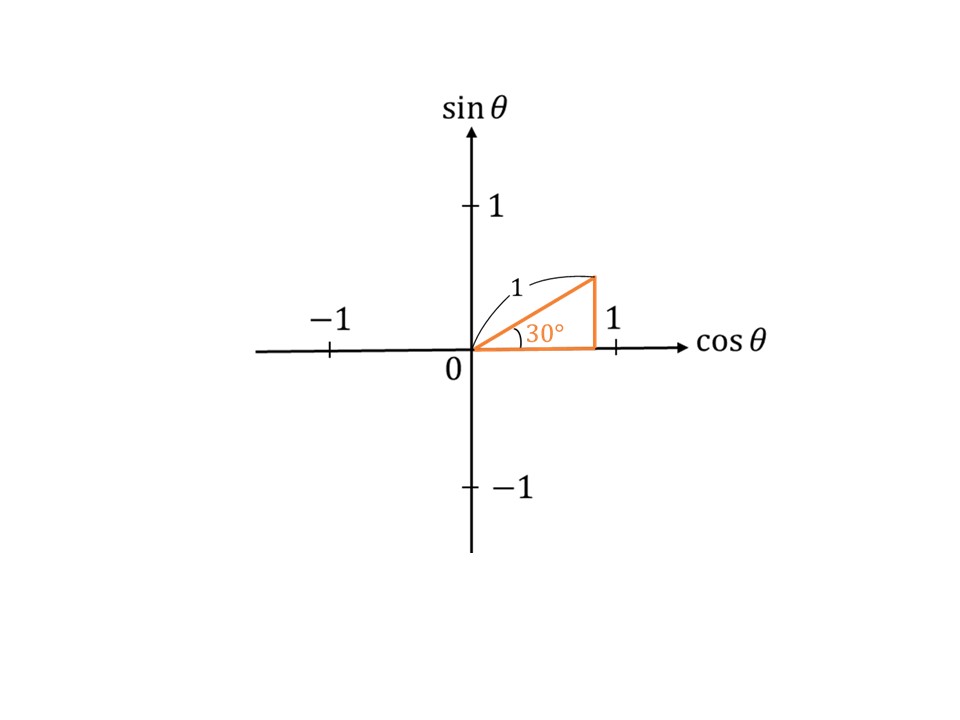
「なぜ$1$にする必要があるの?」
という声が聞こえてきそうですが、それは比だからです!
この単元は三角比でしたよね?
比というのは、何か基準があってその基準に対する値が比です。
例えば、3割と言われれば、全員が 全体が10割のうちの3割 であることが理解できます。それは10割という基準があるからです。%でも同じです。22%と言われれば 全体が100%のうちの22% であることだと瞬時に全員がわかります。つまり、何か基準があれば全員が同じ割合を想像することができるのです。
今回の三角比であれば、$\theta=30°$だけだといろんな相似の三角形を想像することができます。ですが、ここに、直角三角形の斜辺の大きさを$1$としたときという基準を設ければ、全員が同じ三角形を想像することができるようになるのです。これが三角比です。
そして、動径の大きさを$1$にする理由はまだあります!
三角比の定義を思い出してみてください。
$\sin\theta=\frac{y}{r}$
$\cos\theta=\frac{x}{r}$
$\tan\theta=\frac{y}{x}$
これでしたね。動径の大きさが$1$ということは、$r$が$1$ということなので、すなわち、次のように、書き換えることができます。
$\sin\theta=\frac{y}{1}=y$
$\cos\theta=\frac{x}{1}=x$
$\tan\theta=\frac{y}{x}$
すごく見通しがよく、簡単になりましたよね。動径の大きさを$1$にすることでたくさんメリットがあるのです。
そしてそして、もうひとつ!重要なことがあります!
それは、、、
直角三角形の斜辺の大きさが$1$ということは$\theta$がどんな値をとっても、斜辺は常に$1$なので次の図のように、点$(\cos\theta,\sin\theta)$は常に円上に存在することになるのです。この円はもちろん半径の大きさが$1$の円であるので、単位円と呼ばれています。
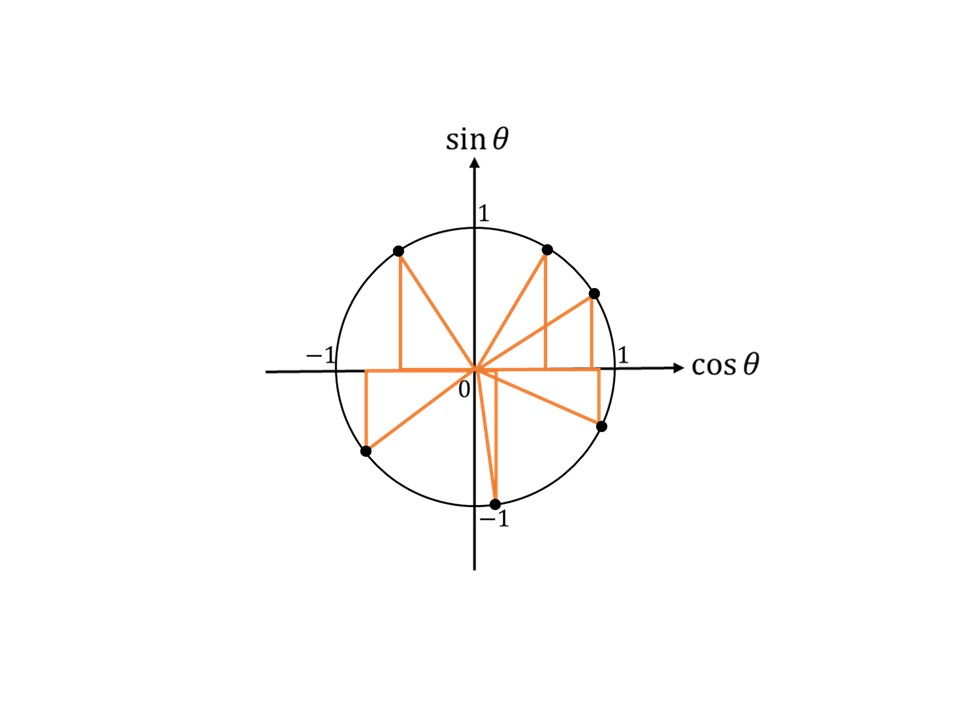
ここまできたらすべてがわかりましたね。
話が長くなってしまいましたが、今、例題の(2)の$\sin30°=\frac{1}{2}$はどういう意味かを考えていました。
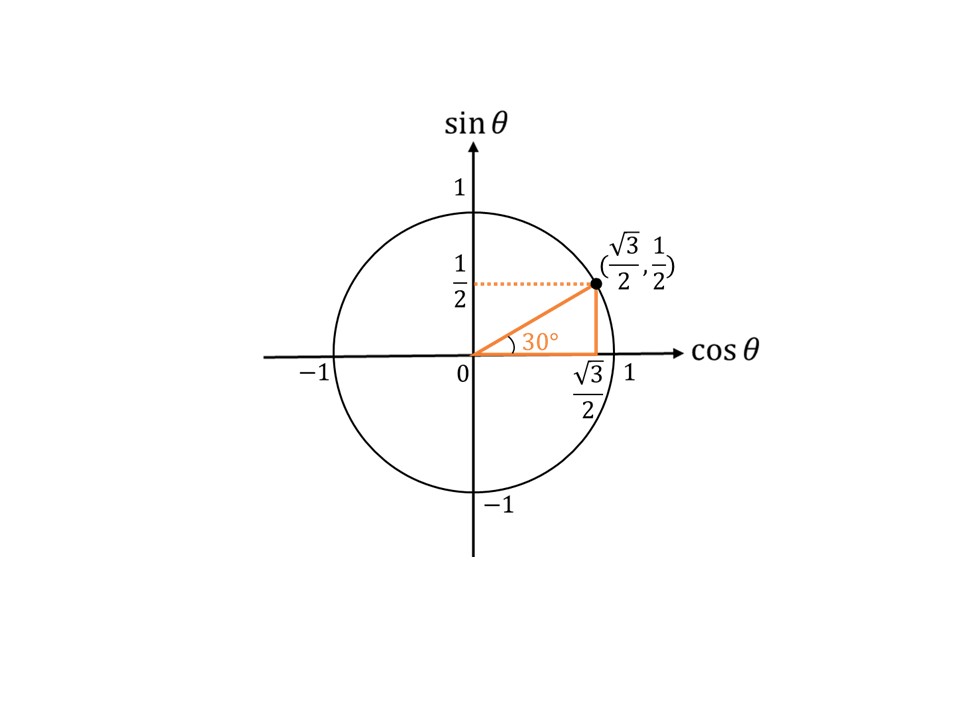
それは、次の図のようなところに点があり、その点から$\sin\theta$軸($y$軸)に向かって垂線をおろしたときの値が、先ほど読み替えた$\sin30°=\frac{1}{2}$は$\theta$が$30°$のときの$y$軸の値は$\frac{1}{2}$ということになるのです。
ちなみにですが、下の図からわかるように$\theta=30°$のとき、$\frac{1}{2}$であることがわかりましたが、このまま$\theta=30°$のとき$\cos\theta$軸に対して垂線を引くと、$\frac{\sqrt{3}}{2}$であることがわかります。つまり、$\cos30°=\frac{\sqrt{3}}{2}$となります。これは例題(7)ですね!
これまで、三角比の全体のイメージとして説明してきました。しかし、数学Ⅰでは主に$0°\leq\theta\leq180°$のみを扱います。そのため、今回のような円全体$(360°)$で考えることは少ないと思いますが、数学Ⅱで円全体$(360°)$に拡張されますので、ぜひ今のうちから円で考えることをおすすめします。
そこでですが、最初に$0$、$1$、$\frac{1}{2}$、$\frac{\sqrt{2}}{2}$、$\frac{\sqrt{3}}{2}$という数は覚えておいて下さいと言いました。それは、有名角または有名角で構成された角のときに$\sin\theta$や$\cos\theta$がとる値なのです。(有名角で構成された角とは例えば$120°$です。$120°=30°+90°$のように有名角で構成することができる角のことをいいます。)
もちろん有名角でない例えば$4°$や$22°$といったときにも先ほど説明したように、直角三角形を作って$\sin\theta$軸や$\cos\theta$軸がとる値を調べることは可能ですが、その場合にはよく教科書の後ろの方に載っている三角比の表が必要です。たとえテストでそのような角が出されても三角比の表が一緒についてきます。ですが、有名角のときの値しか出ない問題では三角比の表はついてこないので、覚える必要があるのです。
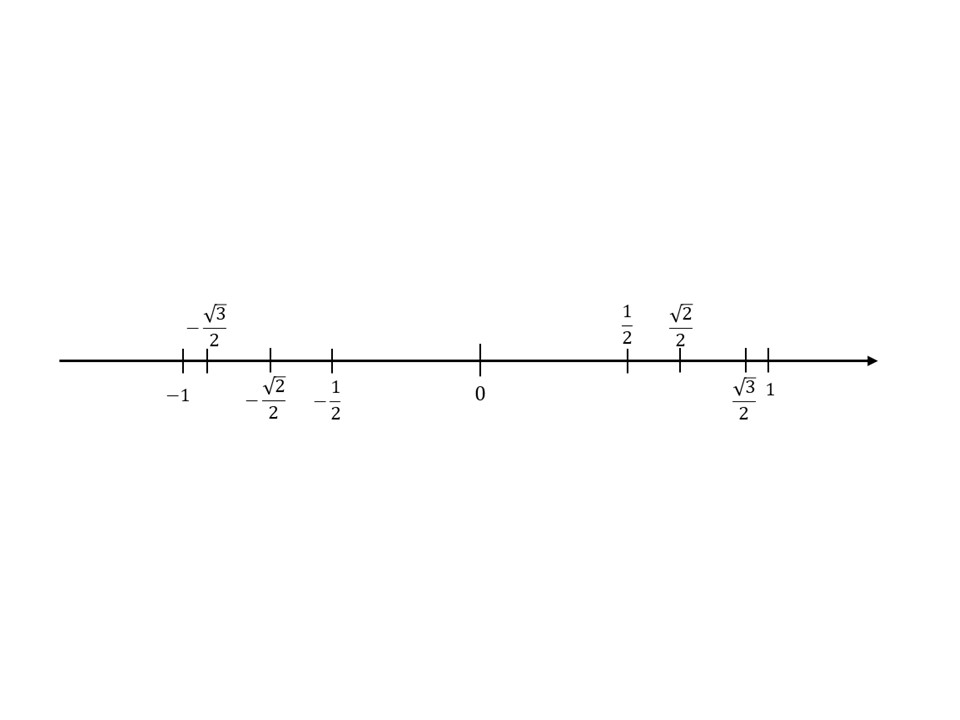
「覚えるのが大変!」と思うかもしれませんが、先ほど大小関係を大事にしてくださいと言いました。それは下の数直線のように、大小関係さえわかっていれば、覚える必要がなくなるんです!
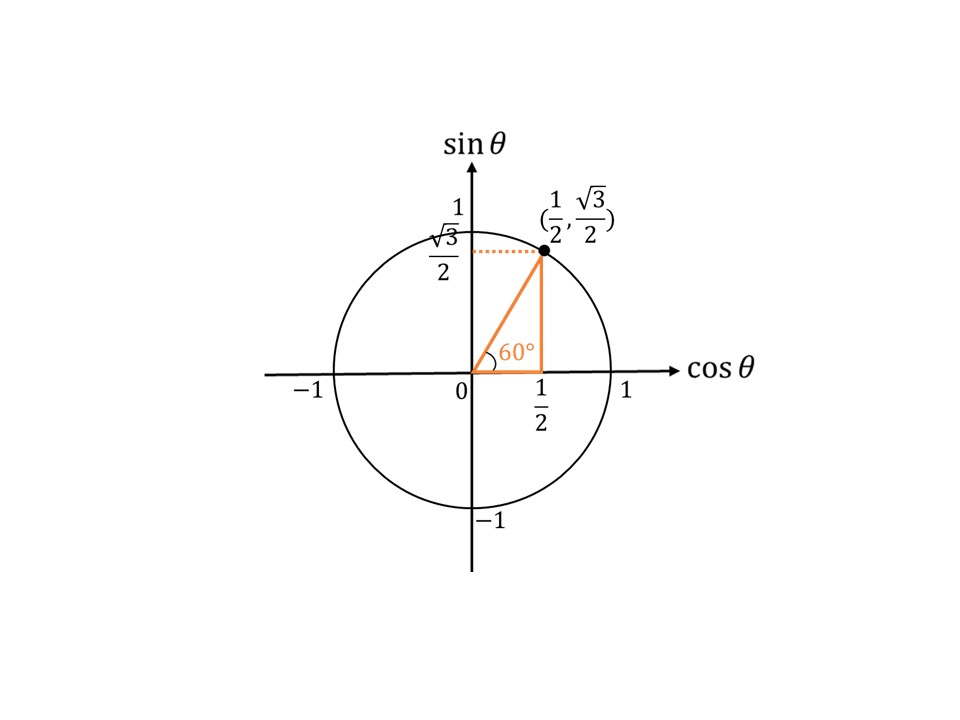
有名角だけであれば、例えば$\sin60°$と言われたとき、頭の中で下の図のように単位円と三角形を描くことさえできたら、そのときの$\sin\theta$軸の大きさと$\cos\theta$軸の大きさを比べたとき、どっちが大きいかわかりますよね。$\sin\theta$軸のとる値の方が、$\cos\theta$軸のとる値よりも大きいです。ということは$\sin60°=\frac{\sqrt{3}}{2}$で$\cos60°=\frac{1}{2}$と瞬時に答えられるようになるのです。
最後に
今回は、三角比の$\sin\theta$と$\cos\theta$について説明しました。次回は$\tan\theta$について説明していきたいと思います。


コメント