こんにちは、シュントです。
今回は、正弦定理と余弦定理について説明していきます。前回まで学んできた、$\sin\theta$や$\cos\theta$を使って遊んでみよう!といった段階です。
まずはじめに、それぞれ正弦定理と余弦定理がどんな定理なのかだけ先に紹介しときます!
正弦定理と余弦定理
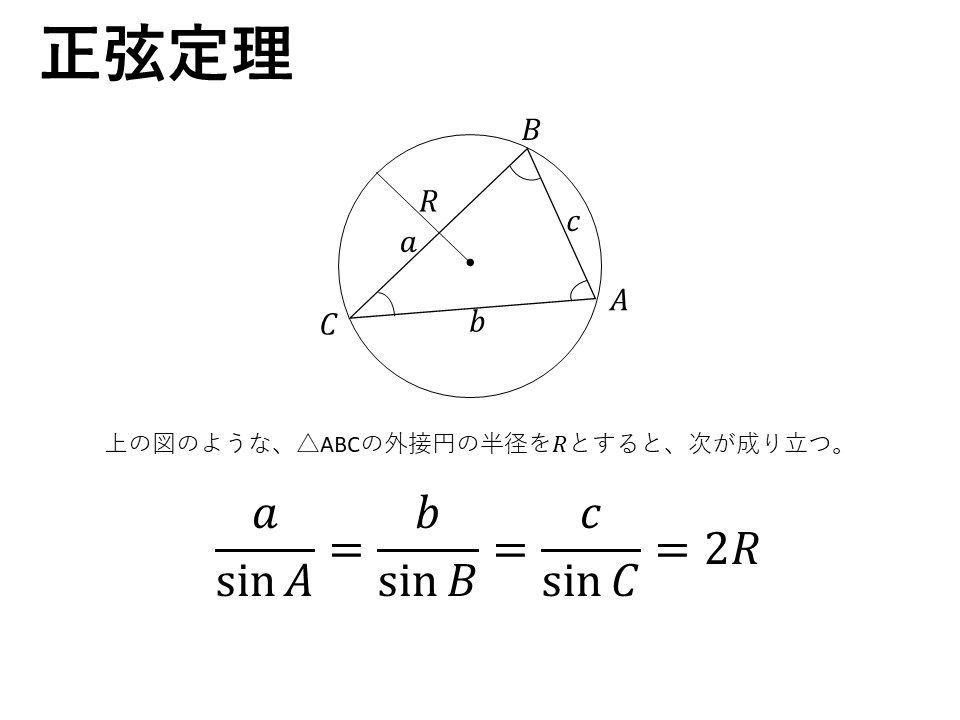
ちなみに、三角形の3つの頂点を通る円を、その三角形の外接円といいます。
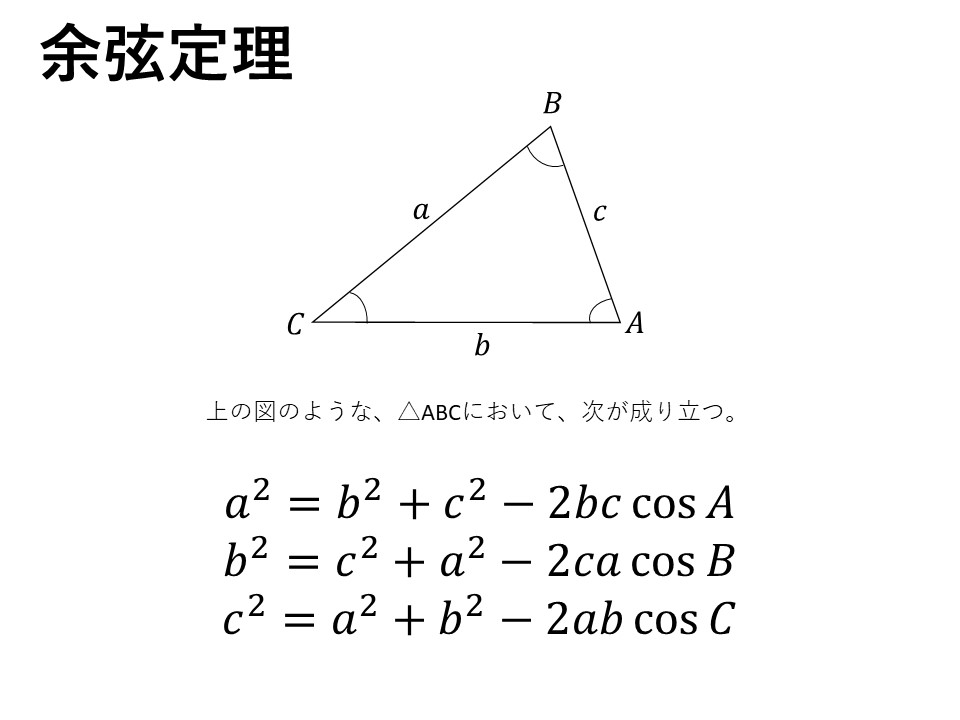
以上です!
定理なので、公式みたいな感じです。高校数学ではめっちゃ使います!特に共通テストとか!
では、これらの定理を使って、どんな問題を解くのか、さっそく例題を通してみていきましょう!
例題と解答

これが例題です!下に解答も載せておきますね!
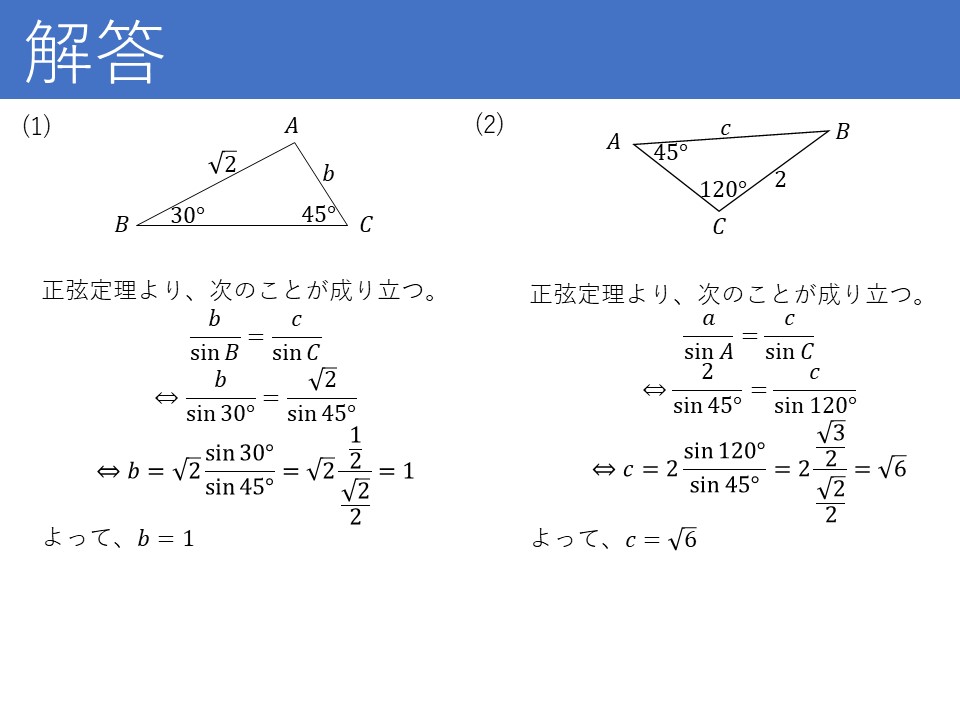
どうでしたか?まずは、正弦定理の例題でした。
「図がないから解けない!」と思われた方もいるのではないでしょうか。
でもたった2問でも何となくわかりましたよね。三角形の頂点に対する辺がそれぞれ対応してるので、図がなくても、全員が同じ三角形を描くことができます。
正弦定理や余弦定理の問題を解くときには、必ず最初に三角形をかいて、どこがどの角度でどこがどの辺なのかを視覚的に確認できるようにしてください。たとえ、ある程度慣れてきても図を描くことをおすすめします。
ではまた別の例題を出します。

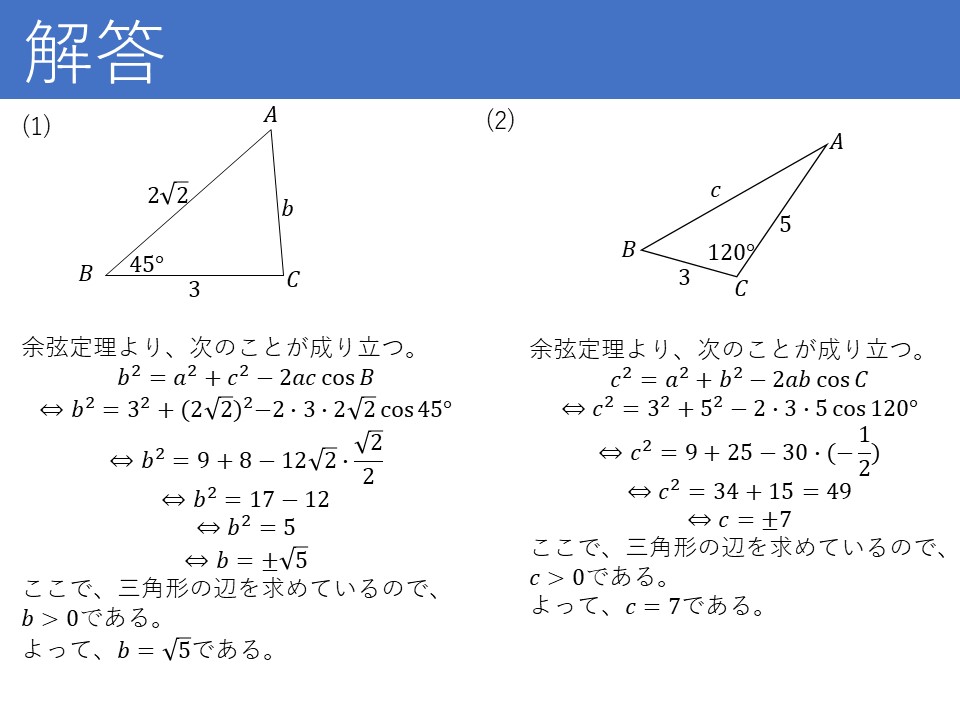
これは余弦定理の例題でした。
正弦定理の例題も余弦定理の問題も何となくどういう使い方をするかわかりましたか?
一旦、例題は終わりです。
では、正弦定理と余弦定理はなんのために理解するのか、そして、どういった意味があるのかということをここで定性的に、また、定量的に説明していきたいと思います!
正弦定理と余弦定理の定性的な捉え方
ここで、正弦定理と余弦定理を定性的に説明していきたいと思います。
まずは、正弦定理です。
三角比を思い出してみてください。正弦定理にも余弦定理にも言えますが、そもそも式に$\sin\theta$や$\cos\theta$が含まれているので三角比と密接に関係しているわけです。
ここで重要なのが直角三角形なんです!
三角比の単元でもお話ししましたが、三角比は直角三角形で定義していました。また、問題を解くとき、単位円を描いて、動径を動かし、直角三角形を作っていました。つまり、直角三角形がカギを握っていることがなんとなくわかってきましたね。
そこで、直角三角形を作るときや、作れるときを考えるんです。なにか思いつきますか?
そのひとつが、円周角の定理です!
円周角の定理にはいくつかありましたよね。その中でも直角三角形のやつです!でわかりますよね(笑)
”定性的に説明”なのでこのくらいラフな説明でいきます。
要は円周角の定理でできた直角三角形の斜辺が直径になっていて、直径に$\sin\theta$を掛ければひとつの辺がわかるよね。
というのが正弦定理なんです!
わかりにくい方は、定量的な説明でしっかりと式と図で説明するので安心してくださいね!
次は、余弦定理です。
もうひとつ、直角三角形と聞いて思い浮かべるものがありますよね。
それは、あの三平方の定理です!直角三角形といえば三平方の定理ですよね~(笑)
そうなんです。余弦定理は”三平方の定理の発展型”と覚えるといいんです!
それはなぜかというと、三平方の定理は主に、直角三角形のみにしか使えませんでしたよね?ですが余弦定理は直角三角形じゃないといけないという制約がなく使えるからなんです。
下の図のように、どの三角形も直角になっている角の角度を変えれば、どんな三角形も作ることができそうですよね?
そして、直角三角形を基準として、$90°$の角を小さくしたり、大きくしたりしたとき、直角三角形での斜辺だった長さは、例えば$-2bc\cos$$A$の割合で変化すると先人は発見したわけです。
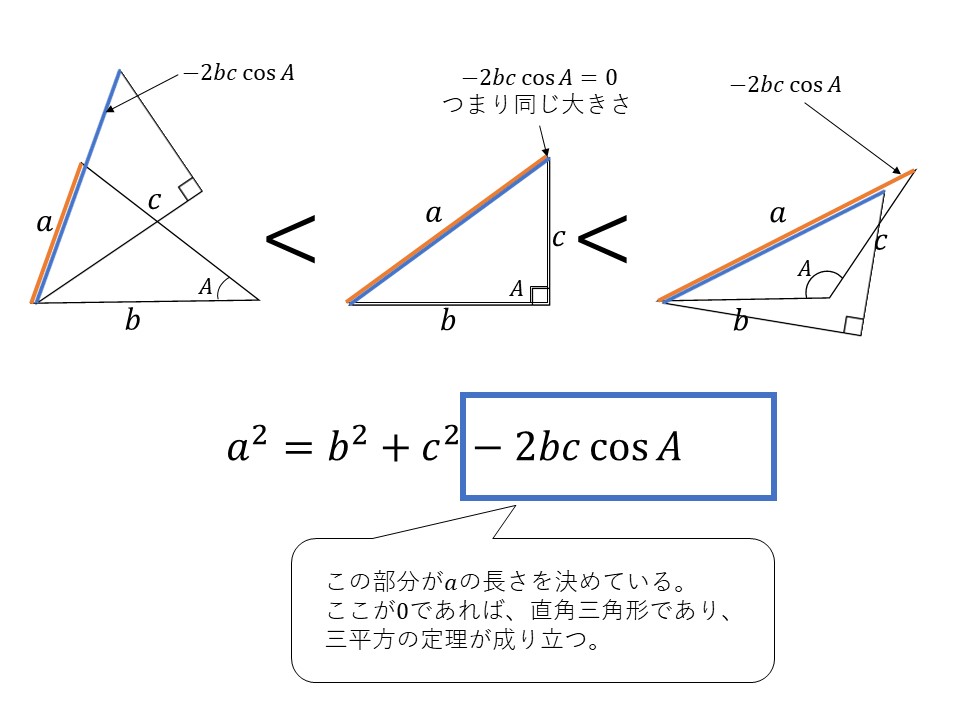
でも、「なぜ$-2bc\cos$$A$の割合で変化するのがわかるの?」と思うかもしれませんがそれを後に説明します。
ということで、今、大まかに伝えるということで定性的に話しました。次は、これらを式、数値や図を使って証明のように、定量的に話していこうと思います。
正弦定理と余弦定理の定量的な捉え方
先ほどお話ししたように、正弦定理では円周角の定理がカギになります。ここでは、円周角の定理の証明はしませんが、次の図のような定理でしたね。
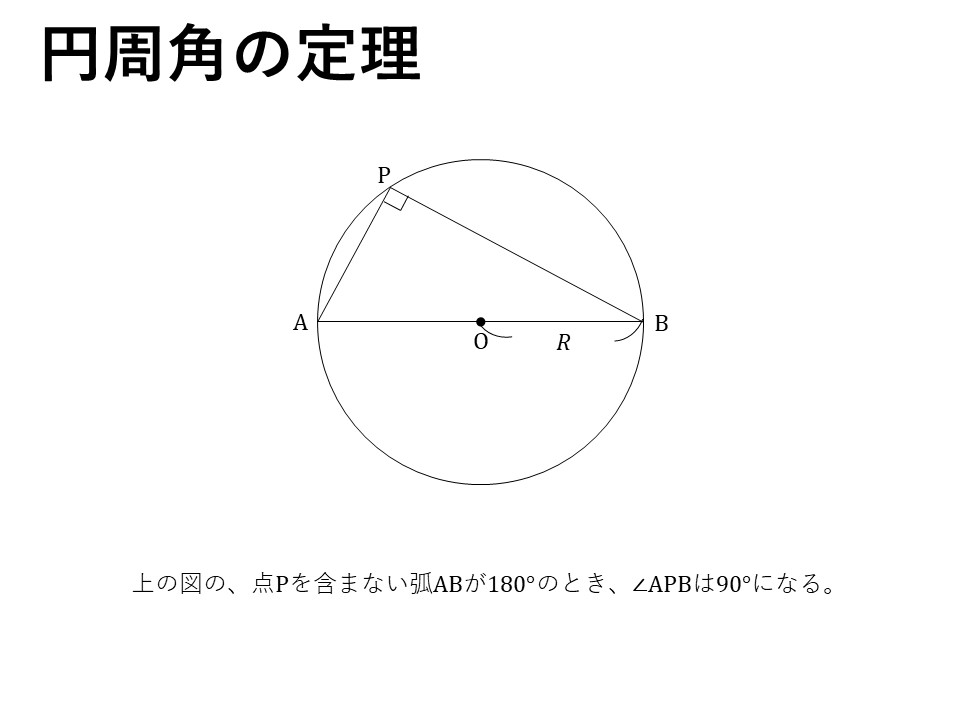
図を見たらすぐに直角三角形になっていることがわかりますね。
この直角三角形が、三角比でもやった、$\sin\theta$軸と$\cos\theta$軸のグラフだと思って考えると、次の図のようになります。
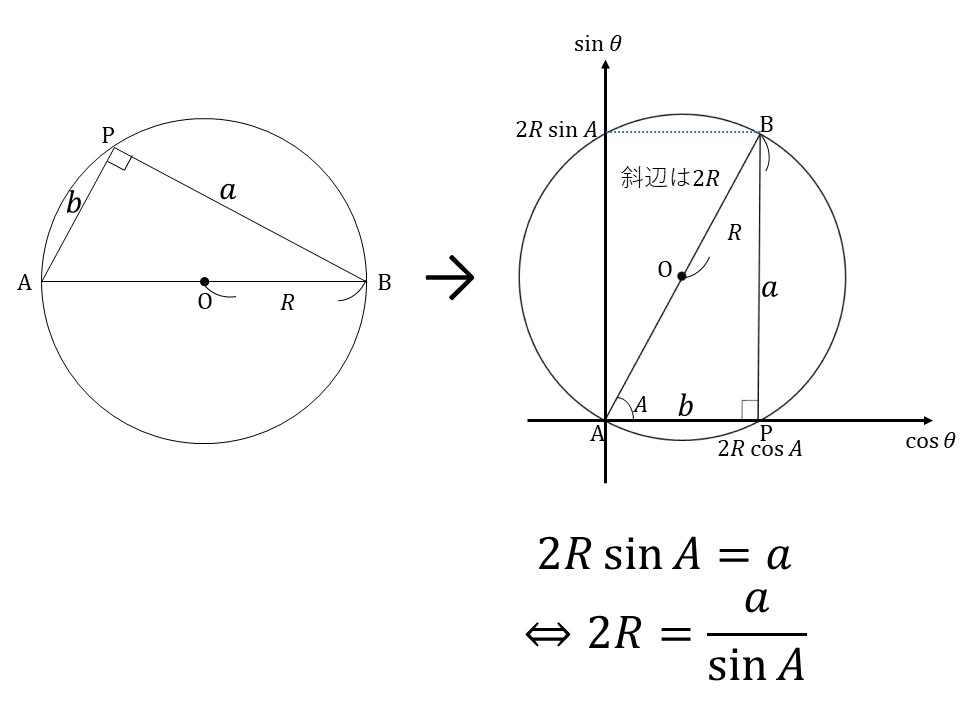
この図から見ると、少しなじみがあるように見えませんか?
そうです!三角比のところでもやったグラフですね!
あとは成り立っているところを確認して、等式をつくるのみです!
つまり、長さが$2R$の斜辺に$\sin$$A$を掛けたものは、動径(大きさは$2R$)を$A$だけ回転させたとき、$0$から、動径から下した垂線と$\sin\theta$軸の交点との大きさが一致するということですね。
$2R\sin\mathit{A}=a$
式を変形すると、
$2R=\frac{a}{\sin\mathit{A}}$
まさに正弦定理が出来上がりましたね!言葉よりも式を見た方がはやいです!
また、$\sin\theta$の定義に従って等式を作ってもよいです。(もちろんやっていることは同じです!)
$\sin\mathit{A}=\frac{a}{2R}$
式を変形すると、
$2R=\frac{a}{\sin\mathit{A}}$
同じ結果になりましたね!
今回、角$A$に着目したため$a$が含まれる正弦定理になります。
どちらにせよ、正弦定理は、円周角の定理よりいつでも直角三角形になるため、この定理が成り立つということが式から理解することができましたね。
次は、余弦定理についてです。
余弦定理では、三平方の定理がカギとなっていましたね。
まず、下の図を見てください。
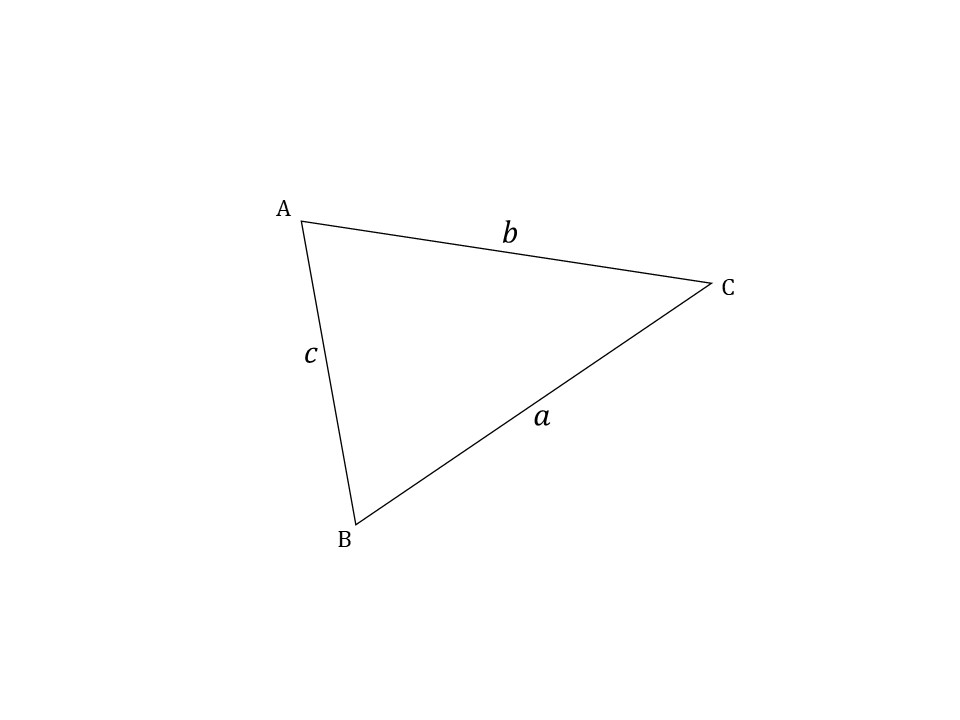
ただの三角形ですよね。たとえばこの三角形の辺のどれかの大きさを知りたいとき、何か関係式があれば求められますよね。しかし、三平方の定理を使うには直角三角形でなくてはいけませんでした。
この三角形の形や大きさを変えずに、直角三角形を作りだすには、次のように補助線を引いてあげるのはどうでしょうか。
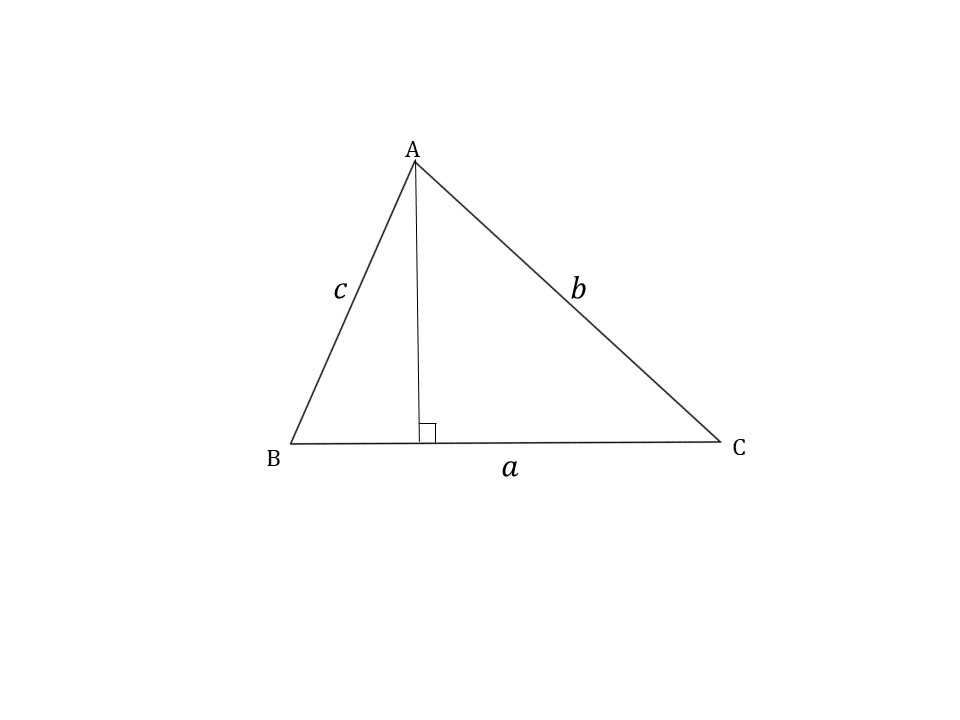
直角三角形が出来上がりましたね。
直角三角形ができれば、あとは三角比の考えた方をするだけです。
こんな感じに、グラフを思い出してみましょう!
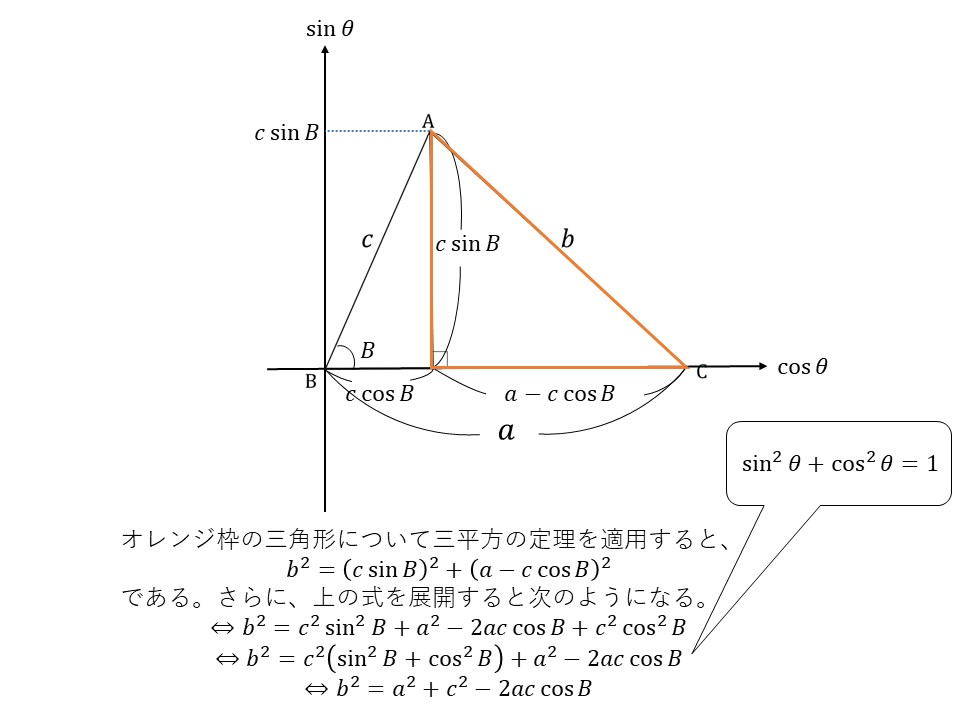
二つの直角三角形があると考えたとき、左の直角三角形は
三角比から、
補助線の大きさが$c\sin\mathit{B}$
底辺($\cos\theta$軸の値)が$c\cos\mathit{B}$
ということがわかります。そして、全体の△ABCで見たときの底辺は$a$だったので、右の直角三角形の底辺の大きさは$a-c\cos\mathit{B}$であるということもわかります。
それらの辺の大きさがわかった上で、オレンジ色の枠の三角形に対して三平方の定理を適用すると、図の下の式のように、余弦定理が導けます。今回、角$B$に着目したため$b^2$からはじまる余弦定理になります。
最後に
今回は、三角比の定義から導ける、正弦定理と余弦定理について説明してきました。正弦定理と余弦定理、もっと言えば、三角比に大切なことは、、
直角三角形
$\sin\theta$と$\cos\theta$のグラフ
であることがだんだんわかってきたはずです!
これらを意識して、この単元には挑みましょう。
そして、実は数学Ⅰでの$\sin\theta$、$\cos\theta$、$\tan\theta$を扱う単元の重要な性質はすべてお話ししました!
あとはたんさん問題を解いたり、応用問題について考えたりするのみです!なので、次回はこの単元の例題をたくさん取り扱おうと考えています!丁寧に解説していくので、一緒に頑張りましょう!


コメント