こんにちは、シュントです。
前回まで、三角比の$\sin\theta$、$\cos\theta$、$\tan\theta$のそれぞれ$0°\leq\theta\leq90°$のときについて説明してきました。
今回は、それを拡張して$0°\leq\theta\leq180°$の場合について考えていきます。
といっても、$0°\leq\theta\leq90°$のときとほとんど同じですので、安心してください!
では、さっそく例題を使って説明しようと思うので、解いてみましょう!
例題と解答
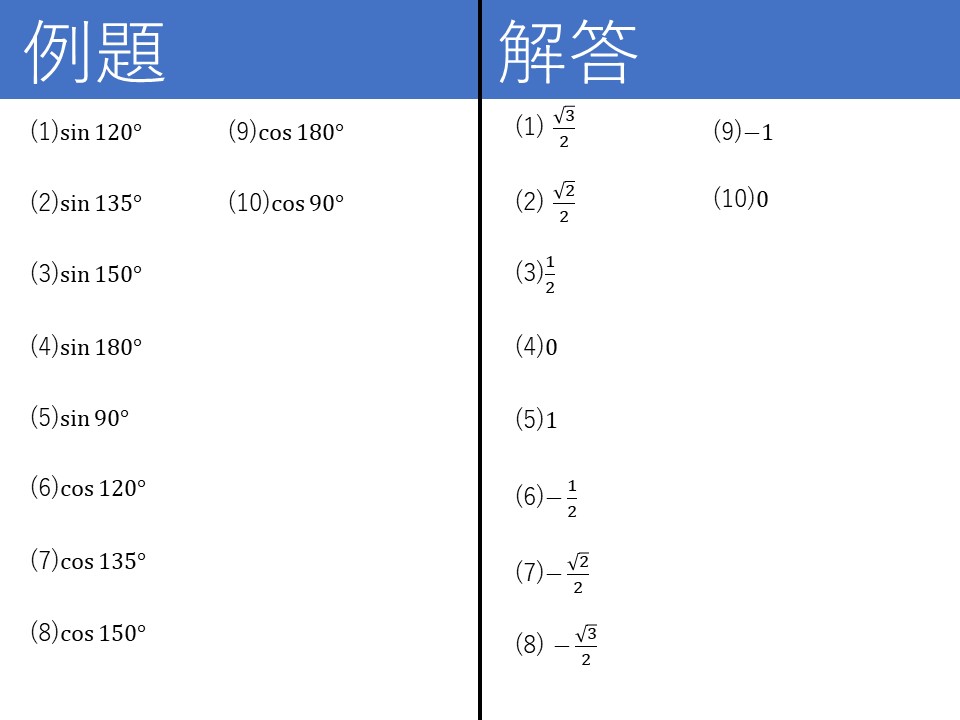
これまでの例題と解答を見てきた人ならならわかるかもしれません。また、同じような答えばかりですよね(笑)。
マイナスがついたくらいで数はすべてみたことあるやつです。
そろそろわかってきたかもしれませんが、本当に三角比では、これらの数字ばっかりが出てくるんですよ。
ただ、角度がすべて$90°$以上なので、わからなかった人もいたかもしれません。ですが、単位円を描けばとても簡単です。実際に例題(1)を取り上げて、どのような手順で解いているかを解説していきますね。
例題(1)の解説
三角比や三角関数では、とにかく単位円のグラフを即時に頭の中で描いていください!
単位円のグラフはこんなんでしたね!
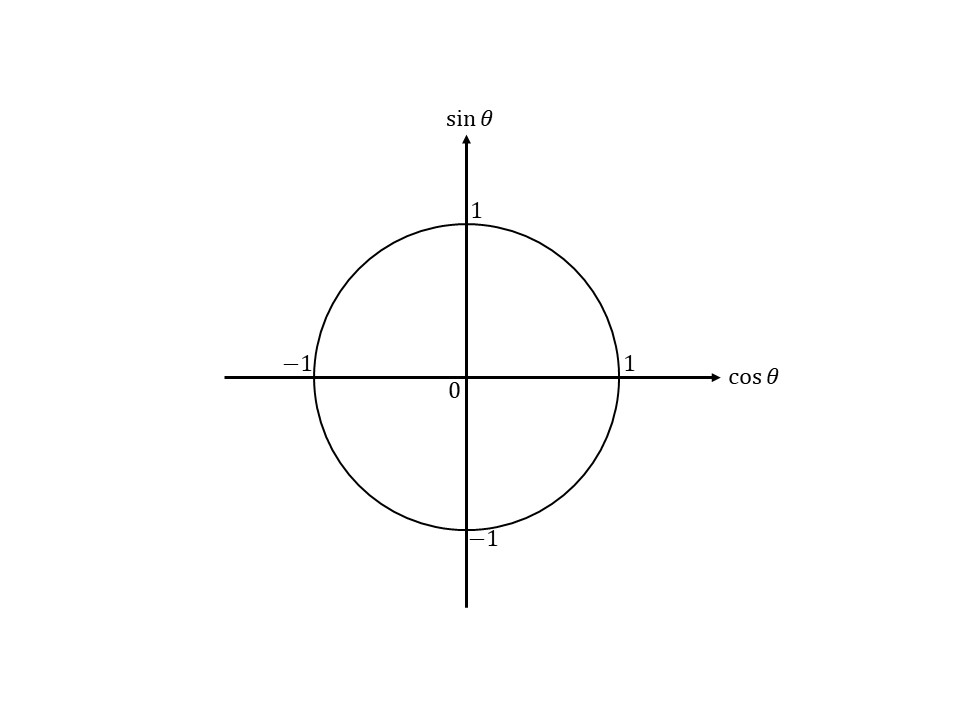
そしたら、次は動径を頭の中で$120°$動かしてみてください。
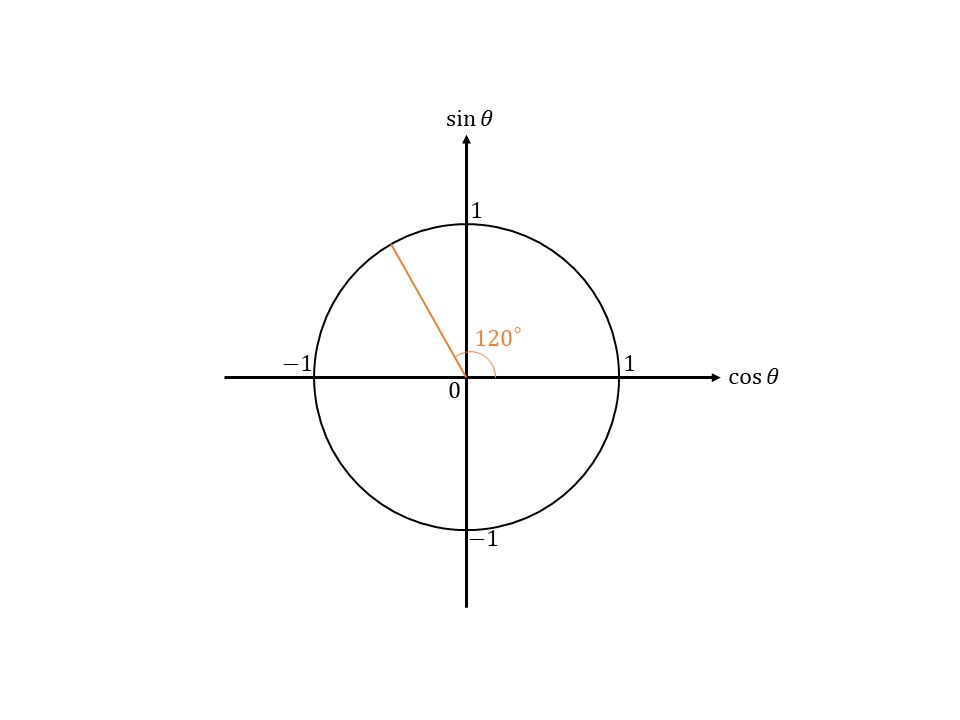
こんなふうに。有名角しかでないので、大体で大丈夫です!
あとは、$0°\leq\theta\leq90°$のときと同じように聞かれている軸、つまり例題(1)では$\sin120°$なので、$\sin\theta$軸に対して垂線を引いてみてください。
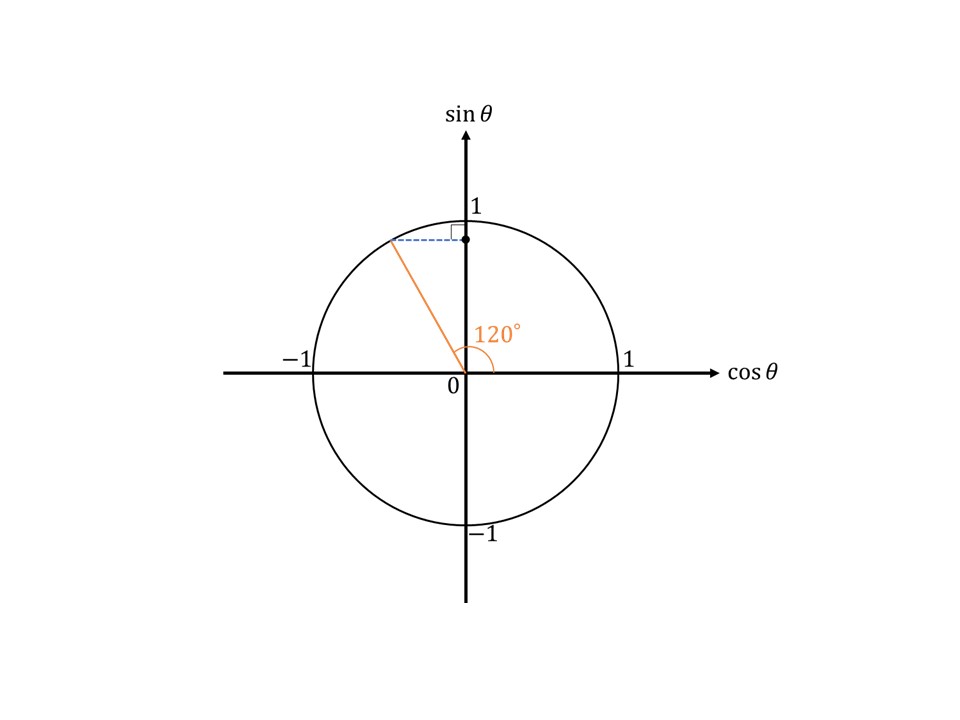
そして、その垂線と$\sin\theta$軸の交点の大きさを下の縦の数直線に照らし合わせてみてください。
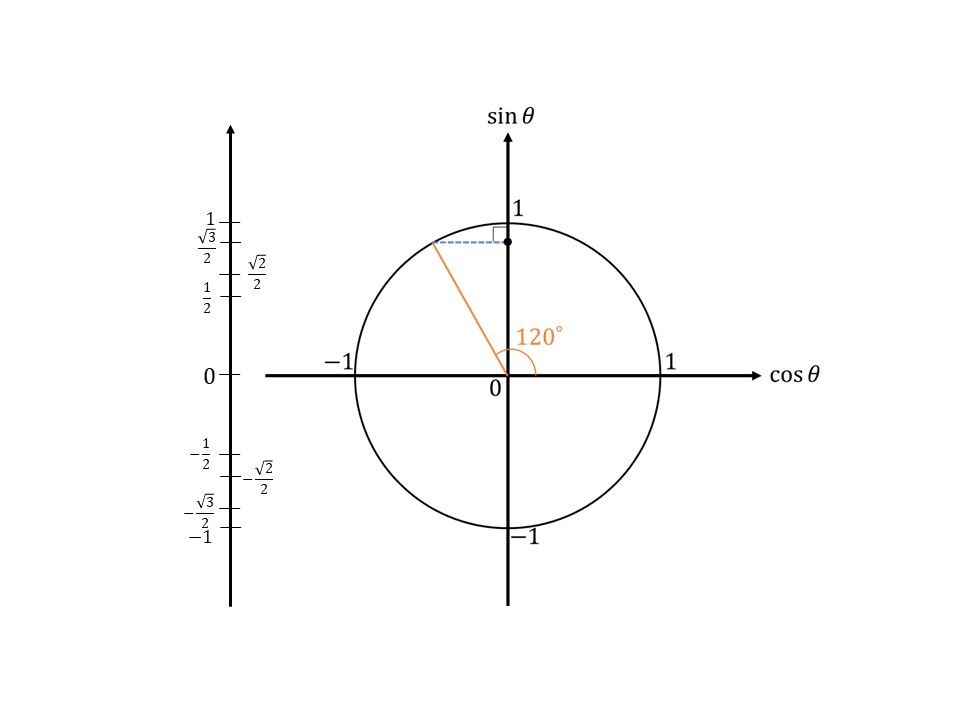
なんとなく$\frac{\sqrt{3}}{2}$あたりですよね。なので、例題(1)の答えは$\frac{\sqrt{3}}{2}$になります。
「そんな大体でいいの?」と思うかもしれませんが、自分で値を求めて答えを導き出すときは、必ず有名角か有名角で構成された角のときしかありません。なのでこのやり方で困ることは一切ありませんので、安心してください。
また、「$120°$って有名角やっけ?」と思われた方いたかもしれませんが、先述にもあるように、$120°$は有名角で構成された角なので、例えば$120°=90°+30°$のように$90°$と$30°$に分けることができます。このとき、単位円は円なので、$90°$回転した後の$30°$と$0°$から回転した$30°$は、値の+か-かは変わるかもしれませんが、考え方は同じように使えるので、有名角のときと同じように扱えるわけです。
そして、ここで気付いた人はすごいです!
「$120°=90°+30°$という分け方以外にも$120°=180°-60°$もいけるやん!」って
そうなんです!別に分け方に答えはありません。有名角や有名角で構成された角であれば、自分の好きなように分けることができます。つまり、動径を一度、$180°$回転させて、$60°$戻したと考えても良いわけです。
要するに、
$120°=90°+30°$
$120°=180°-60°$
上の$30°$や$60°$の部分が有名角になっていれば私たちは、
$-1$、$-\frac{\sqrt{3}}{2}$、$-\frac{\sqrt{2}}{2}$、$-\frac{1}{2}$、$0$、$\frac{1}{2}$、$\frac{\sqrt{2}}{2}$、$\frac{\sqrt{3}}{2}$、$1$
のどれかと知っているので答えられるようになるということなんです。
実は教科書では、この有名角で構成された角を有名角に変換する公式が載っています。しかしこれは絶対に覚えるということはしないでください。この公式をすぐにかけるようになるやり方を紹介します。
有名角で構成された角を有名角に変換する公式
とりあえず、教科書に載っているように公式を紹介します。ですが、覚えないでくださいね。
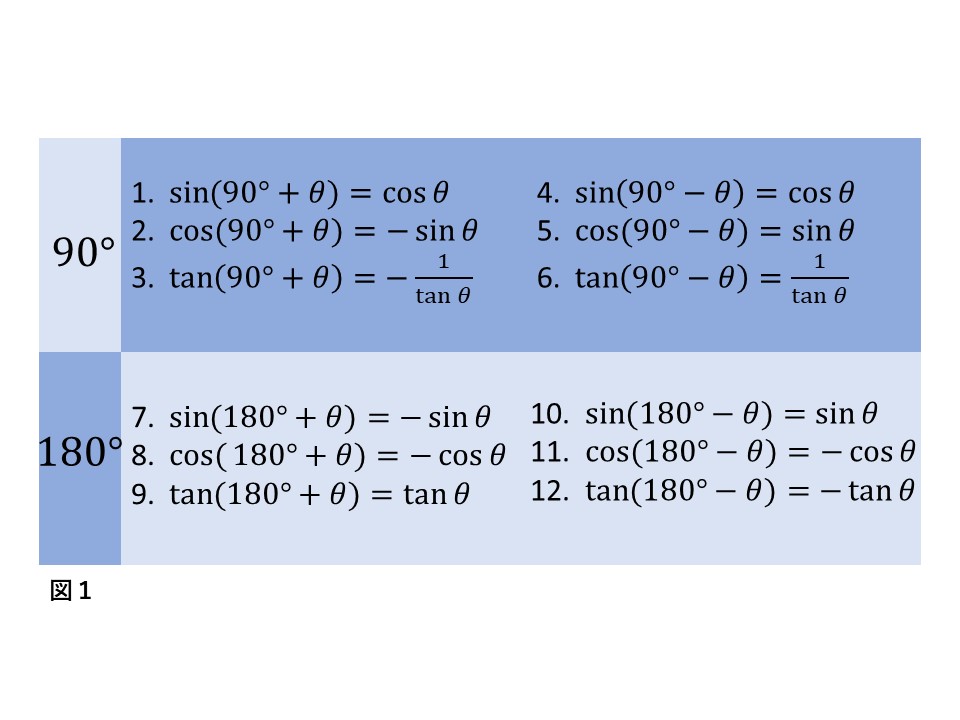
てか、絶対覚えたくないですよね(笑)
なので、この公式を使えるようになるには、次のことだけを覚えてください。
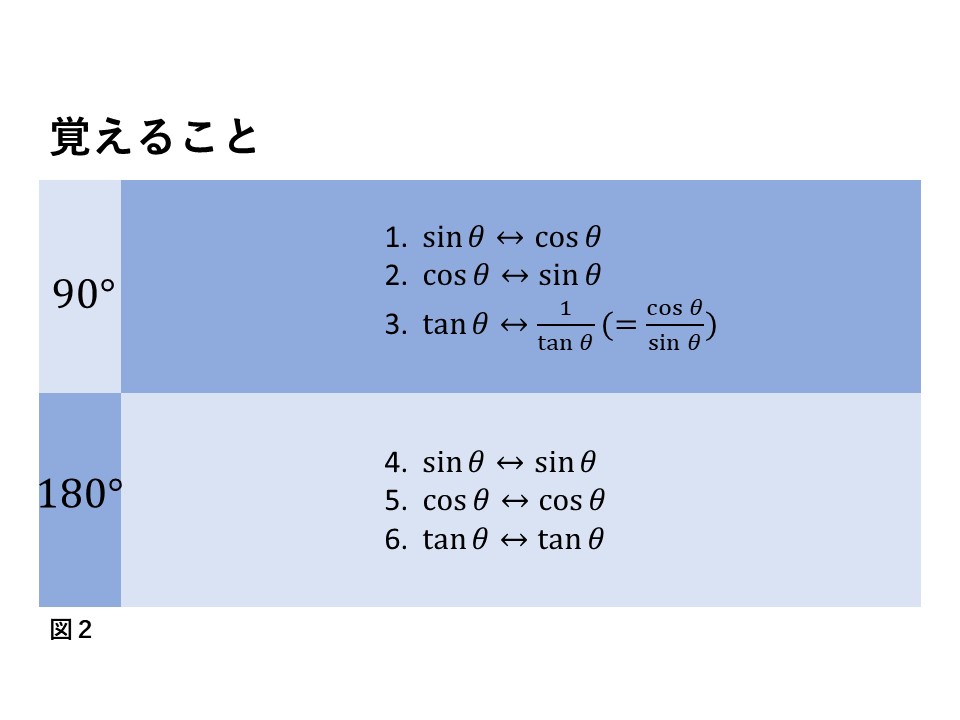
これは、さすがに覚えられますね。意味はこれから順を追って説明していきます。
例えば図1の式1の公式、つまり、$\sin(90°+\theta)$がどうなるのか知りたいとしましょう。その場合、次の順で求めてください。
①符号を決定する。
②$90°$か$180°$かを確かめて記号(sinθ、cosθ、tanθ)を決定する。
です。
①では何をするかというと、頭の中で次のような図を思い浮かべてください。ここで、$\theta$の範囲は鋭角、つまり、$0°\leq\theta\leq90°$の適当な角です。$0°\leq\theta\leq90°$の理由は基本的な有名角($0°$、$30°$、$45°$、$60°$、$90°$)はこの範囲だからです。
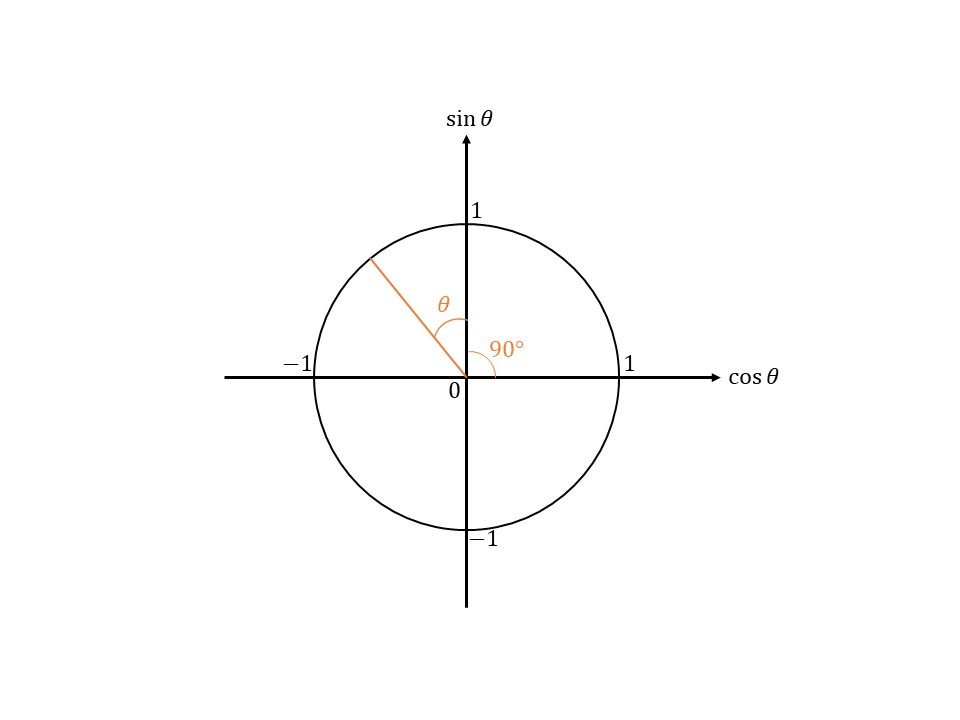
こんな感じになりましたか?動径を$90°$回転させて、さらに、$+\theta$回転させたようなグラフです。
では、このとき、動径が示す$\sin\theta$軸の符号はなんですか?
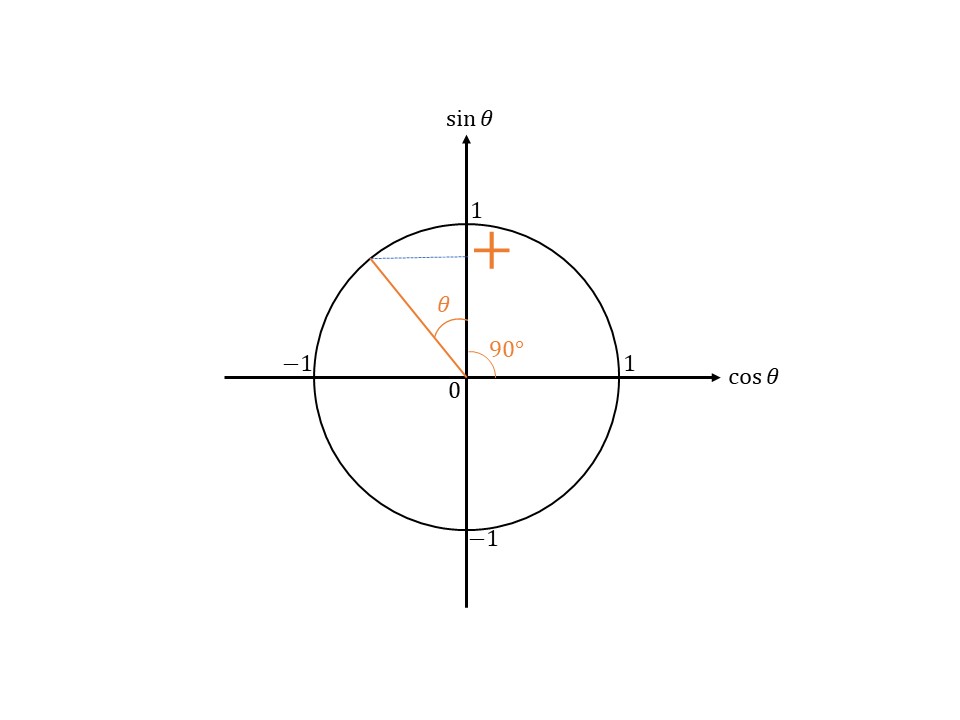
上の図からわかるように、正($+$)ですよね。なので、符号は$+$で決定です。
②では何をするかというと、図2で覚えたやつです。今回$\sin(90°+\theta)$ですので、図2の$90°$の方の$\sin\theta$を見てください。すると、
$\sin\theta↔\cos\theta$
と書かれていますね。なので、記号は$\cos\theta$で決定です。
①の$+$と②の$\cos\theta$を合わせて、$\sin(90°+\theta)$は$+\cos\theta$、すなわち$\cos\theta$になることがわかりました。
図1の式1を見てみるとそうなっていますよね。
どうでしたか?簡単でしたよね。
一応もう一つくらいやっておきますね。図1の式12をやってみます。
まずは、次のように、動径を$180°$回転させて、さらに$-\theta$回転させたグラフを想像してくださいね。
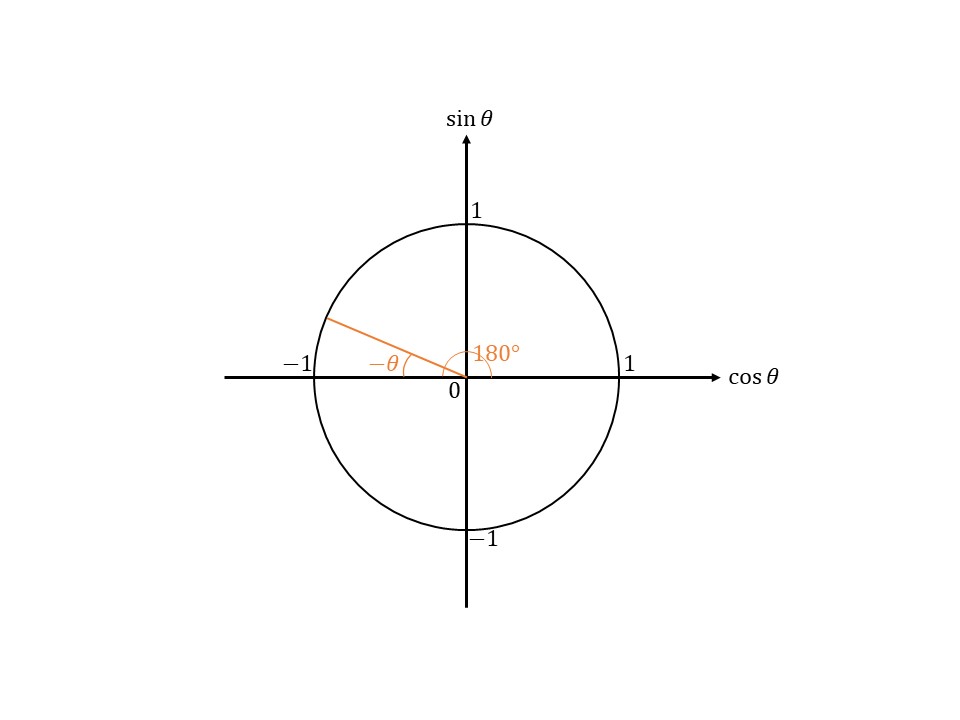
そしたら①です。符号を決めますが、$\tan(180°-\theta)$のときはどうしたよいかというと傾きが正か負かで判断します。(傾きではなく、$\tan(180°-\theta)=\frac{\sin(180°-\theta)}{\cos(180°-\theta)}$と考えてそれぞれ$\sin(180°-\theta)$と$\cos(180°-\theta)$)の符号を考えてもできます。)
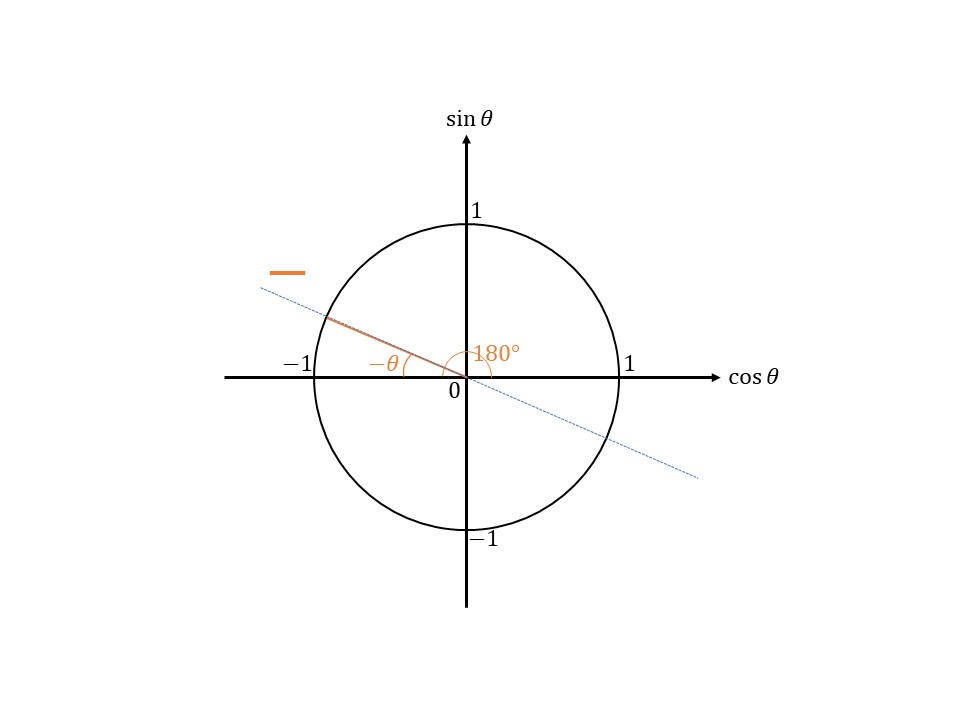
上の図のようになるので、傾きは負($-$)ですね。
次に②です。図2の式6を見てください。すると、
$\tan\theta↔\tan\theta$
と書かれていますね。なので、記号は$\tan\theta$で決定です。
①の$-$と②の$\tan\theta$を合わせて、$\tan(180°-\theta)$は$-\tan\theta$になることがわかりました。
図1の式12を見てみるとそうなっていますね。
このようにして、どの場合がきてもすべてグラフで対応できますので、公式を覚えるのではなく、三角比の性質的に公式を習得しましょう!
最後に
これまで、三角比を$0°\leq\theta\leq180°$に拡張したときにどう解いていくかを説明してきました。
次回は正弦定理と余弦定理についてやっていこうと思います!



コメント